
【题目】在平面直角坐标系xOy中,对于点Pa,b和点Qa,b,给出如下定义:若![]() ,则称点Q为点P的限变点,例如:点(2,3)的限变点的坐标是(2,3),点2,5的限变点的坐标是2,5。
,则称点Q为点P的限变点,例如:点(2,3)的限变点的坐标是(2,3),点2,5的限变点的坐标是2,5。
(1)在点A2,1,B1,2中有一个点是函数y=![]() 图象上某一个点的限变点,这个点是 ;
图象上某一个点的限变点,这个点是 ;
(2)求点![]() ,1的限变点的坐标;
,1的限变点的坐标;
(3)若点P在函数yx32xk,k2的图象上,其限变点Q的纵坐标b的取值范围是5b2,求k的取值范围。
【答案】(1)B1,2
()(![]() ,1);
,1);
(3)5≤k≤8.
【解析】
(1)点(-1,-2)在反比例函数图象上,点(-1,-2)的限变点为(-1,2),据此得到答案;
(2)直接根据限变点的定义直接得出答案;
(3)根据题意可知y=-x+3(x≥-2)图象上的点P的限变点必在函数y=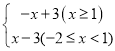 的图象上,结合图象即可得到答案;
的图象上,结合图象即可得到答案;
解:(1)∵A2,1的限变点是(,),它不在反比例函数图象上,
∴点A2,1不符合题意
∵B1,2的限变点是(,),且(,)在反比例函数图象上,
∴这个点是B1,2
()根据限变点的定义可知点(![]() ,1)的限变点的坐标为(
,1)的限变点的坐标为(![]() ,1);
,1);
(3)依题意,y=-x+3(x≥-2)图象上的点P的限变点必在函数y=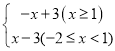 的图象上.
的图象上.
∴b′≤2,即当x=1时,b′取最大值2.
当b′=-2时,-2=-x+3.
∴x=5.
当b′=-5时,-5=x-3或-5=-x+3.
∴x=-2或x=8.
∵-5≤b′≤2,
由图象可知,k的取值范围是5≤k≤8.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】“姹紫嫣红苗木种植基地”尝试用单价随天数而变化的销售模式销售某种果苗,利用30天时间销售一种成本为10元/株的果苗,售后经过统计得到此果苗,单价在第x天(x为整数)销售的相关信息,如下图表所示:
销售量n(株) |
|
销售单价 m(元/株) | 当1≤x≤20时,m=________ |
当21≤x≤30时, |
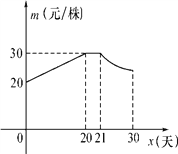
(1)①请将表中当1≤x≤20时,m与x间关系式补充完整;
②计算第几天该果苗单价为25元/株?
(2)求该基地销售这种果苗30天里每天所获利润y(元)关于x(天)的函数关系式;
(3)“吃水不忘挖井人”,为回馈本地居民,基地负责人决定将这30天中,其中获利最多的那天的利润全部捐出,进行“精准扶贫”。试问:基地负责人这次为“精准扶贫”捐赠多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
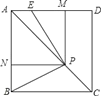
【题目】如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN;
(3)若点P在线段AC上移动,其他不变,设PC=x,AE=y,求y关于x的解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
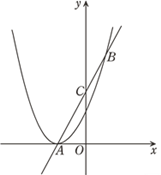
【题目】如图,抛物线y1=ax2+2ax+1与![]() 轴有且仅有一个公共点A,经过点A的直线y2=kx+b交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
轴有且仅有一个公共点A,经过点A的直线y2=kx+b交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
(1)求![]() 的值;
的值;
(2)求直线AB对应的函数解析式;
(3)直接写出当y1 ≥y2 时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
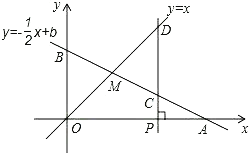
【题目】如图,已知函数y-![]() xb的图象与x轴、y轴分别交于点A、B,与函数yx的图象交于点M,点M的横坐标为2,在x轴上有一点Pa,0(其中a2),过点P作x轴的垂线,分别交函数y
xb的图象与x轴、y轴分别交于点A、B,与函数yx的图象交于点M,点M的横坐标为2,在x轴上有一点Pa,0(其中a2),过点P作x轴的垂线,分别交函数y![]() xb和yx的图象于点C、D.
xb和yx的图象于点C、D.
(1)求点M的坐标;
(2)求点A的坐标;
(3)若OBCD,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
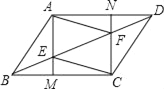
【题目】如图,已知平行四边形ABCD,过A点作AM⊥BC于M,交BD于E,过C点作CN⊥AD于N,交BD于F,连接AF、CE.
(1)求证:四边形AECF为平行四边形;
(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.例如:1423,
,那么称这个四位数为“和平数”.例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是_________________,最大的“和平数”是_______________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC.
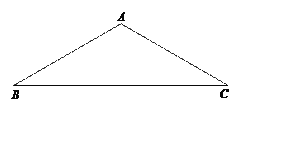
(1)用尺规作出圆心在直线BC上,且过A、C两点的⊙O;(注:保留作图痕迹,标出点O,并写出作法)
(2)若∠B=30°,求证:AB与(1)中所作⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com