【题目】下图是昌平区2019年1月份每天的最低和最高气温，观察此图，下列说法正确的是（ ）
A.在1月份中，最高气温为10℃，最低气温为－2℃
B.在10号至16号的气温中，每天温差最小为7℃
C.每天的最高气温均高于0℃，最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
科目：初中数学 来源： 题型：
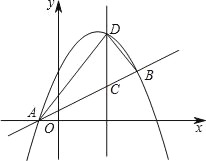
【题目】如图，抛物线y=ax2+bx+
与直线AB交于点A（﹣1，0），B（4，），点D是抛物线A、B两点间部分上的一个动点（不与点A、B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BD．
（1）求抛物线的表达式；
（2）设点D的横坐标为m，△ADB的面积为S，求S关于m的函数关系式，并求出当S取最大值时的点C的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，CE∥BF，CE=BF．则添加下列条件还不能使△EAC≌△FDB．（ ）
A. AB=CDB. AE∥DFC. ∠E=∠FD. AE=DF
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图：O是直线AB上一点，∠AOC＝50°,OD是∠BOC的角平分线，OE⊥OC于点O.求∠DOE的度数.（请补全下面的解题过程）
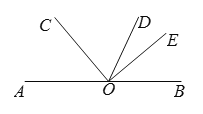
解：∵O是直线AB上一点，∠AOC＝50°，
∴∠BOC＝180°－∠AOC＝ °.
∵ OD是∠BOC的角平分线，
∴∠COD＝ ∠BOC .( )
∴∠COD＝65°.
∵OE⊥OC于点O，（已知）.
∴∠COE＝ °.( )
∴∠DOE＝∠COE－∠COD＝ ° .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列两个等式：
，
给出定义如下：我们称使等式a﹣b＝2ab﹣1成立的一对有理数a，b为“同心有理数对”，记为（a，b），如：数对（1，
），（2，
），都是“同心有理数对”.
（1）数对（﹣2，1），（3，
）是 “同心有理数对”的是__________.
（2）若（a，3）是“同心有理数对”，求a的值；
（3）若（m，n）是“同心有理数对”，则（﹣n，﹣m） “同心有理数对”（填“是”或“不是”），说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
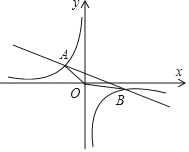
【题目】如图，反比例函数y=
（k≠0）的图象与一次函数y=﹣
x+1的图象交于A（﹣2，m），B（n，﹣1）两点．
（1）求反比例函数的解析式；
（2）连接OA，OB，求△AOB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，点A，B，C是数轴上的三个点，其中AB＝12，且A，B两点表示的数互为相反数.
（1）请在数轴上标出原点O，并写出点A表示的数；
（2）如果点Q以每秒2个单位的速度从点B出发向左运动，那么经过 秒时，点C恰好是BQ的中点；
（3）如果点P以每秒1个单位的速度从点A出发向右运动，那么经过多少秒时PC＝2PB.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在四边形ABCD中，AD∥BC，∠A=∠C，点P在边AB上．
（1）求证：四边形ABCD是平行四边形；
（2）若AB=AD，以过点P的直线为轴，将四边形ABCD折叠，使点B、C分别落在点B′、C′上，且B′C′经过点D，折痕与四边形的另一交点为Q．在图2中作出四边形PB′C′Q（保留作图痕迹，不必说明作法和理由）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于E，两线相交于F点．
（1）若∠BAC=60°，∠C=70°，求∠AFB的大小；
（2）若D是BC的中点，∠ABE=30°，求证：△ABC是等边三角形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
