
【题目】如图所示,点A,B,C是数轴上的三个点,其中AB=12,且A,B两点表示的数互为相反数.
![]()
(1)请在数轴上标出原点O,并写出点A表示的数;
(2)如果点Q以每秒2个单位的速度从点B出发向左运动,那么经过 秒时,点C恰好是BQ的中点;
(3)如果点P以每秒1个单位的速度从点A出发向右运动,那么经过多少秒时PC=2PB.
【答案】(1)见解析,-6;(2)8;(3)20或![]()
【解析】
(1)根据AB=12,且A,B两点表示的数互为相反数,可得A、B两点表示的数分别是﹣6和6;
(2)根据C是BQ的中点可得出BQ=2BC,由(1)得点C表示的是﹣2的点,则BC=8,则BQ=2BC=16,点Q以每秒2个单位的速度从点B出发向左运动,所需时间为![]() 秒;
秒;
(3)设经过t秒PC=2PB,此时PC=![]() ,
,![]() ,列出关于t的方程即可解出答案.
,列出关于t的方程即可解出答案.
解:(1)根据AB=12,且A,B两点表示的数互为相反数,可得A、B两点表示的数分别是﹣6和6,则图中每个小格代表两个单位长度,画出点O如图所示:
![]()
所以:正确标出原点O,点A表示的数是-6.
(2)∵C是BQ的中点,
∴BQ=2BC;
由(1)得点C表示的数是﹣2,
则:BC=8,
∴BQ=2BC=16
∵点Q以每秒2个单位的速度从点B出发向左运动,
∴所需时间为![]() 秒
秒
故答案为:8秒
(3)设经过t秒PC=2PB.
由已知,经过t秒,点P在数轴上表示的数是-6+t.
∴PC=![]() =
=![]() ,
, ![]() .
.
∵![]() .
.
∴![]() ,解得:t=20或
,解得:t=20或![]()
∴t=20或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
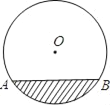
【题目】某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
(1)①∠BCE与∠CDF的大小关系是_______________;
②证明:GF⊥BF;
(2)探究G落在边DC的什么位置时,BF=BC,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)

解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°-∠AOC= °.
∵ OD是∠BOC的角平分线,
∴∠COD= ∠BOC .( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE-∠COD= ° .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题背景
折纸是一种许多人熟悉的活动,将折纸的一边二等分、四等分都是比较容易做到的,但将一边三等分就不是那么容易了,近些年,经过人们的不懈努力,已经找到了多种将正方形折纸一边三等分的精确折法,最著名的是由日本学者芳贺和夫发现的三种折法,现在被数学界称之为芳贺折纸三定理.其中,芳贺折纸第一定理的操作过程及内容如下(如图1):
操作1:將正方形ABCD对折,使点A与点D重合,点B与点C重合.再将正方形ABCD展开,得到折痕EF;
操作2:再将正方形纸片的右下角向上翻折,使点C与点E重合,边BC翻折至B'E的位置,得到折痕MN,B'E与AB交于点P.则P即为AB的三等分点,即AP:PB=2:1.

解决问题
(1)在图1中,若EF与MN交于点Q,连接CQ.求证:四边形EQCM是菱形;
(2)请在图1中证明AP:PB=2:l.
发现感悟
若E为正方形纸片ABCD的边AD上的任意一点,重复“问题背景”中操作2的折纸过程,请你思考并解决如下问题:
(3)如图2.若![]() =2.则
=2.则![]() = ;
= ;
(4)如图3,若![]() =3,则
=3,则![]() = ;
= ;
(5)根据问题(2),(3),(4)给你的启示,你能发现一个更加一般化的结论吗?请把你的结论写出来,不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 城气象台测得台风中心在
城气象台测得台风中心在![]() 城正西方向
城正西方向![]() 的
的![]() 处,以每小时
处,以每小时![]() 的速度向南偏东
的速度向南偏东![]() 的
的![]() 方向移动,距台风中心
方向移动,距台风中心![]() 的范围内是受台风影响的区域.
的范围内是受台风影响的区域.

(1)求![]() 城与台风中心之间的最小距离;(2)求
城与台风中心之间的最小距离;(2)求![]() 城受台风影响的时间有多长?
城受台风影响的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F在菱形ABCD的对边上,AE⊥BC.∠1=∠2.
(1)判断四边形AECF的形状,并证明你的结论.
(2)若AE=4,AF=2,试求菱形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交快速通道开通后,为响应市政府“绿色出行”的号召,家住新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶多少千米?
.小王用自驾车方式上班平均每小时行驶多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com