
【题目】综合与实践
问题背景
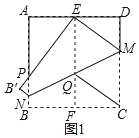
折纸是一种许多人熟悉的活动,将折纸的一边二等分、四等分都是比较容易做到的,但将一边三等分就不是那么容易了,近些年,经过人们的不懈努力,已经找到了多种将正方形折纸一边三等分的精确折法,最著名的是由日本学者芳贺和夫发现的三种折法,现在被数学界称之为芳贺折纸三定理.其中,芳贺折纸第一定理的操作过程及内容如下(如图1):
操作1:將正方形ABCD对折,使点A与点D重合,点B与点C重合.再将正方形ABCD展开,得到折痕EF;
操作2:再将正方形纸片的右下角向上翻折,使点C与点E重合,边BC翻折至B'E的位置,得到折痕MN,B'E与AB交于点P.则P即为AB的三等分点,即AP:PB=2:1.

解决问题
(1)在图1中,若EF与MN交于点Q,连接CQ.求证:四边形EQCM是菱形;
(2)请在图1中证明AP:PB=2:l.
发现感悟
若E为正方形纸片ABCD的边AD上的任意一点,重复“问题背景”中操作2的折纸过程,请你思考并解决如下问题:
(3)如图2.若![]() =2.则
=2.则![]() = ;
= ;
(4)如图3,若![]() =3,则
=3,则![]() = ;
= ;
(5)根据问题(2),(3),(4)给你的启示,你能发现一个更加一般化的结论吗?请把你的结论写出来,不要求证明.
【答案】(1)见解析;(2)见解析;(3)4;(4)6;(5)见解析.
【解析】分析:(1)由折叠可得,CM=EM,∠CMQ=∠EMQ,四边形CDEF是矩形,由CM=EQ,CM∥QE,可证四边形EQCM是平行四边形,进而证明四边形EQCM是菱形;
(2)设正方形ABCD的边长为1,CM=x,则EM=x,DM=1﹣x,在Rt△DEM中,由勾股定理可求得x的值,由△AEP∽△DME,列比例式求出AP的值,进而求出PB的值,从而结论可求;
(3)设正方形ABCD的边长为1,CM=x,则EM=x,DM=1﹣x,在Rt△DEM中,由勾股定理可得x的值,由△AEP∽△DME,可得AP的值和BP的值,进而求得结论.
(4)与(3)相同的方法求解即可;
(5)与(3)相同的方法求解即可;
详解:(1)由折叠可得,CM=EM,∠CMQ=∠EMQ,四边形CDEF是矩形,
∴CD∥EF,
∴∠CMQ=∠EQM,
∴∠EQM=∠EMQ,
∴ME=EQ,
∴CM=EQ,
又∵CM∥QE,
∴四边形EQCM是平行四边形,
又∵CM=EM,
∴四边形EQCM是菱形;
(2)如图1,设正方形ABCD的边长为1,CM=x,则EM=x,DM=1﹣x,
在Rt△DEM中,由勾股定理可得:EM2=ED2+DM2,
即x2=(![]() )2+(1﹣x)2,解得x=
)2+(1﹣x)2,解得x=![]() ,
,
∴CM=![]() ,DM=
,DM=![]() ,
,
∵∠PEM=∠D=90°,
∴∠AEP+∠DEM=90°,∠DEM+∠EMD=90°,
∴∠AEP=∠DME,
又∵∠A=∠D=90°,
∴△AEP∽△DME,
∴![]() =
=![]() ,即
,即![]() ,解得AP=
,解得AP=![]() ,
,
∴PB=![]() ,
,
∴AP:PB=2:l.
(3)如图2,设正方形ABCD的边长为1,CM=x,则EM=x,DM=1﹣x,
在Rt△DEM中,由勾股定理可得:EM2=ED2+DM2,
即x2=(![]() )2+(1﹣x)2,解得x=
)2+(1﹣x)2,解得x=![]() ,
,
即CM=![]() ,
,
∴DM=![]() ,
,
由△AEP∽△DME,可得
![]() =
=![]() ,即
,即 ,解得AP=
,解得AP=![]() ,
,
∴PB=![]() ,
,
∴![]() =4,
=4,
故答案为:4;
(4)如图3,同理可得AP=![]() ,PB=
,PB=![]() ,
,
∴![]() =6,
=6,
故答案为:6;
(5)根据问题(2),(3),(4),可得当![]() (n为正整数),则
(n为正整数),则![]() .
.
理由:设正方形ABCD的边长为1,CM=x,则EM=x,DM=1﹣x,
在Rt△DEM中,由勾股定理可得:EM2=ED2+DM2,
即x2=(![]() )2+(1﹣x)2,解得x=
)2+(1﹣x)2,解得x=![]() ,
,
∴DM=1﹣CM=![]() ,
,
由△AEP∽△DME,可得
![]() =
=![]() ,即
,即 ,解得AP=
,解得AP=![]() ,
,
∴PB=![]() ,
,
∴![]() .
.




科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共
共![]() 个区,
个区, ![]() 区是边长为
区是边长为![]() 的正方形,
的正方形, ![]() 区是边长为
区是边长为![]() 的正方形.
的正方形.
(1)列式表示每个![]() 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果![]() ,
, ![]() ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
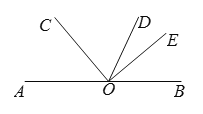
【题目】如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)
解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°-∠AOC= °.
∵ OD是∠BOC的角平分线,
∴∠COD= ∠BOC .( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE-∠COD= ° .
查看答案和解析>>
科目:初中数学 来源: 题型:
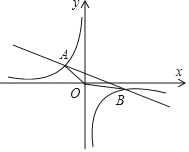
【题目】如图,反比例函数y=![]() (k≠0)的图象与一次函数y=﹣
(k≠0)的图象与一次函数y=﹣![]() x+1的图象交于A(﹣2,m),B(n,﹣1)两点.
x+1的图象交于A(﹣2,m),B(n,﹣1)两点.
(1)求反比例函数的解析式;
(2)连接OA,OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A,B,C是数轴上的三个点,其中AB=12,且A,B两点表示的数互为相反数.
![]()
(1)请在数轴上标出原点O,并写出点A表示的数;
(2)如果点Q以每秒2个单位的速度从点B出发向左运动,那么经过 秒时,点C恰好是BQ的中点;
(3)如果点P以每秒1个单位的速度从点A出发向右运动,那么经过多少秒时PC=2PB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图平面直角坐标系中,O(0,0),A(4,4![]() ),B(8,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(8,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则CE:DE的值是 .
,则CE:DE的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上.
(1)求证:四边形ABCD是平行四边形;
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
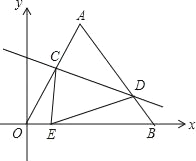
【题目】如图,经过点A(6,0)的直线y=kx﹣3与直线y=﹣x交于点B,点P从点O出发以每秒1个单位长度的速度向点A匀速运动.
(1)求点B的坐标;
(2)当△OPB是直角三角形时,求点P运动的时间;
(3)当BP平分△OAB的面积时,直线BP与y轴交于点D,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国庆节社会实践活动中,盐城某校甲、乙、丙三位同学一起调查了高峰时段盐靖高速、盐洛高速和沈海高速的车流量(每小时通过观测点的汽车车辆数),三位同学汇报高峰时段的车流量情况如下:
甲同学说:“盐靖高速车流量为每小时2000辆.”
乙同学说:“沈海高速的车流量比盐洛高速的车流量每小时多400辆.”
丙同学说:“盐洛高速车流量的5倍与沈海高速车流量的差是盐靖高速车流量的2倍.”
请你根据他们所提供的信息,求出高峰时段盐洛高速和沈海高速的车流量分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com