
【题目】如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)
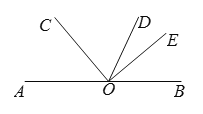
解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°-∠AOC= °.
∵ OD是∠BOC的角平分线,
∴∠COD= ∠BOC .( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE-∠COD= ° .
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有三点 A,B,C ,若用 AB 表示 A,B 两点的距离,AC 表示 A ,C 两点的 距离,且 BC 2 AB ,点 A 、点C 对应的数分别是a 、c ,且| a 20 | | c 10 | 0 .
![]()
(1)若点 P,Q 分别从 A,C 两点同时出发向右运动,速度分别为 2 个单位长度/秒、5个单位长度/ 秒,则运动了多少秒时,Q 到 B 的距离与 P 到 B 的距离相等?
(2)若点 P ,Q 仍然以(1)中的速度分别从 A ,C 两点同时出发向右运动,2 秒后,动点 R 从 A点出发向左运动,点 R 的速度为1个单位长度/秒,点 M 为线段 PR 的中点,点 N为线段 RQ的中点,点R运动了x 秒时恰好满足 MN AQ 25,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用方程解答下列问题
(1)一件工作,甲单独做20小时完成,乙单独做12小时完成,现在先由甲单独做4小时,余下的由甲乙一起完成余下的部分需要几小时完成?
(2)王强参加了一场3000米的赛跑,他以6米/秒的速度跑了一段路程,又以4米/秒的速度跑完了其余的路程,一共花了10分钟,王强以6米秒的速度跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图各图是棱长为1cm的小正方体摆成的,如图①中,从正面看有1个正方形,表面积为6cm2;如图②中,从正面看有3个正方形,表面积为18cm2;如图③,从正面看有6个正方形,表面积为36cm2;…
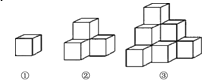
(1)第6个图中,从正面看有多少个正方形?表面积是多少?
(2)第n个图形中,从正面看有多少个正方形?表面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
(1)①∠BCE与∠CDF的大小关系是_______________;
②证明:GF⊥BF;
(2)探究G落在边DC的什么位置时,BF=BC,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题背景
折纸是一种许多人熟悉的活动,将折纸的一边二等分、四等分都是比较容易做到的,但将一边三等分就不是那么容易了,近些年,经过人们的不懈努力,已经找到了多种将正方形折纸一边三等分的精确折法,最著名的是由日本学者芳贺和夫发现的三种折法,现在被数学界称之为芳贺折纸三定理.其中,芳贺折纸第一定理的操作过程及内容如下(如图1):
操作1:將正方形ABCD对折,使点A与点D重合,点B与点C重合.再将正方形ABCD展开,得到折痕EF;
操作2:再将正方形纸片的右下角向上翻折,使点C与点E重合,边BC翻折至B'E的位置,得到折痕MN,B'E与AB交于点P.则P即为AB的三等分点,即AP:PB=2:1.

解决问题
(1)在图1中,若EF与MN交于点Q,连接CQ.求证:四边形EQCM是菱形;
(2)请在图1中证明AP:PB=2:l.
发现感悟
若E为正方形纸片ABCD的边AD上的任意一点,重复“问题背景”中操作2的折纸过程,请你思考并解决如下问题:
(3)如图2.若![]() =2.则
=2.则![]() = ;
= ;
(4)如图3,若![]() =3,则
=3,则![]() = ;
= ;
(5)根据问题(2),(3),(4)给你的启示,你能发现一个更加一般化的结论吗?请把你的结论写出来,不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
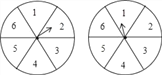
【题目】现有一项资助贫困生的公益活动由你来主持,每位参与者需交赞助费5元,活动规则如下:如图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形,参与者转动这两个转盘,转盘停止后,指针各自指向一个数字,(若指针在分格线上,则重转一次,直到指针指向某一数字为止),若指针最后所指的数字之和为12,则获得一等奖,奖金20元;数字之和为9,则获得二等奖,奖金10元;数字之和为7,则获得三等奖,奖金为5元;其余均不得奖;此次活动所集到的赞助费除支付获奖人员的奖金外,其余全部用于资助贫困生的学习和生活;
(1)分别求出此次活动中获得一等奖、二等奖、三等奖的概率;
(2)若此次活动有2000人参加,活动结束后至少有多少赞助费用于资助贫困生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com