
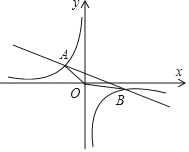
【题目】如图,反比例函数y=![]() (k≠0)的图象与一次函数y=﹣
(k≠0)的图象与一次函数y=﹣![]() x+1的图象交于A(﹣2,m),B(n,﹣1)两点.
x+1的图象交于A(﹣2,m),B(n,﹣1)两点.
(1)求反比例函数的解析式;
(2)连接OA,OB,求△AOB的面积.
【答案】(1)y=-![]() ;(2)3.
;(2)3.
【解析】分析:(1)把A(﹣2,m)代入y=﹣![]() x+1求出点A的坐标,再把点A的坐标代入y=
x+1求出点A的坐标,再把点A的坐标代入y=![]() 求出反比例函数解析式;
求出反比例函数解析式;
(2)把点B(n,﹣1)代入反比例函数y=﹣![]() ,求出点B的坐标,设一次函数y=﹣
,求出点B的坐标,设一次函数y=﹣![]() x+1的图象与x轴的交点为C,根据S△AOB=S△AOC+S△BOC求解即可.
x+1的图象与x轴的交点为C,根据S△AOB=S△AOC+S△BOC求解即可.
详解:(1)因为点A(﹣2,m)在一次函数y=﹣![]() x+1的图象上,
x+1的图象上,
∴m=﹣![]() ×(﹣2)+1=2
×(﹣2)+1=2
即点A(﹣2,2)
∵点A(﹣2,2)在反比例函数y=![]() (k≠0)的图象上,
(k≠0)的图象上,
∴k=(﹣2)×2=﹣4.
所以反比例函数解析式为:y=﹣![]() ;
;
(2)∵点B(n,﹣1)在反比例函数y=﹣![]() ,
,
∴n×(﹣1)=4,
∴点B的坐标为(4,﹣1)
设一次函数y=﹣![]() x+1的图象与x轴的交点为C,
x+1的图象与x轴的交点为C,
当y=0时,﹣![]() x+1=0,
x+1=0,
解得x=2.
∴点C的坐标为(2,0)
所以S△AOB=S△AOC+S△BOC=![]() ×2×2+
×2×2+![]() ×2×1=3.
×2×1=3.



 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
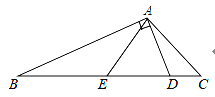
【题目】如图,在△ABC中,∠C=2∠B,点D为BC上一点,且AD⊥AB,点E是BD的中点,连接AE,且AE=DE.
(1)求证:∠AEC=∠C;
(2)若AE=8.5,AD=8,求△ABE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图各图是棱长为1cm的小正方体摆成的,如图①中,从正面看有1个正方形,表面积为6cm2;如图②中,从正面看有3个正方形,表面积为18cm2;如图③,从正面看有6个正方形,表面积为36cm2;…
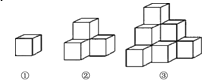
(1)第6个图中,从正面看有多少个正方形?表面积是多少?
(2)第n个图形中,从正面看有多少个正方形?表面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
查看答案和解析>>
科目:初中数学 来源: 题型:
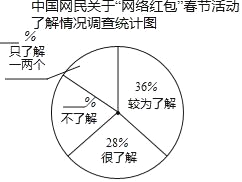
【题目】“网络红包”是互联网运营商、商家通过组织互联网线上活动、派发红包的互联网工具,是朋友间互道祝福的表达形式之一.“网络红包”春节活动已经逐渐深入到大众的生活中,得到了人们较为广泛的关注.根据某咨询公司(2018年中国春节“网络红包”专题调查报告》显示:在接受调查的8万名网民中,对“网络红包”春节话动了解程度的占比方面,“较为了解”和“很了解”的网民共占比64%,分别占比36%和28%.在“不了解”和“只了解一两个“的受访网民中,“不了解”的网民人数比“只了解一两个”的网民人数多25%.如图是该咨询公司绘制的“中国网民关于‘网络红包’春节活动了解情况调查”统计图(不完整).
请根据以上信息解答下列问题:
(1)在受访的网民中,“不了解”和“只了解一两个”的网民人数共有 万人,其中“不了解”的网民人数是 万人;
(2)请将扇形统计图补充完整;
(3)2017除夕晚上小聪和爸爸、妈妈一起玩微信抢红包游戏,他们约定由爸爸在家人微信群中先后发两次“拼手气红包”,每次发放的红包数是3个,每个红包抽到的金额随机(每两个红包的金额都不相等),每次谁抽到红包的金额最大谁就是“手气最佳”者,求两次游戏中小聪都能获得“手气最佳”的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题背景
折纸是一种许多人熟悉的活动,将折纸的一边二等分、四等分都是比较容易做到的,但将一边三等分就不是那么容易了,近些年,经过人们的不懈努力,已经找到了多种将正方形折纸一边三等分的精确折法,最著名的是由日本学者芳贺和夫发现的三种折法,现在被数学界称之为芳贺折纸三定理.其中,芳贺折纸第一定理的操作过程及内容如下(如图1):
操作1:將正方形ABCD对折,使点A与点D重合,点B与点C重合.再将正方形ABCD展开,得到折痕EF;
操作2:再将正方形纸片的右下角向上翻折,使点C与点E重合,边BC翻折至B'E的位置,得到折痕MN,B'E与AB交于点P.则P即为AB的三等分点,即AP:PB=2:1.

解决问题
(1)在图1中,若EF与MN交于点Q,连接CQ.求证:四边形EQCM是菱形;
(2)请在图1中证明AP:PB=2:l.
发现感悟
若E为正方形纸片ABCD的边AD上的任意一点,重复“问题背景”中操作2的折纸过程,请你思考并解决如下问题:
(3)如图2.若![]() =2.则
=2.则![]() = ;
= ;
(4)如图3,若![]() =3,则
=3,则![]() = ;
= ;
(5)根据问题(2),(3),(4)给你的启示,你能发现一个更加一般化的结论吗?请把你的结论写出来,不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点C是直线AB上一点,AC=6cm,BC=4cm,点M、N分别是AC、BC的中点;
(1)如图,点C在线段AB上,求线段MN的长;
(2)若点C在线段AB的延长线上,其他条件不变,则线段MN的长为_______cm.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,再以PE、PC为边作平行四边形PCQE,求对角线PQ的最小值为______________.
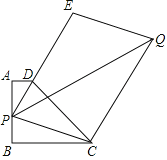
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com