
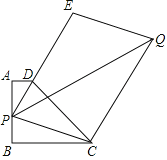
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,再以PE、PC为边作平行四边形PCQE,求对角线PQ的最小值为______________.
科目:初中数学 来源: 题型:
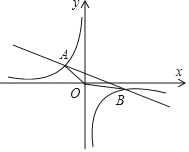
【题目】如图,反比例函数y=![]() (k≠0)的图象与一次函数y=﹣
(k≠0)的图象与一次函数y=﹣![]() x+1的图象交于A(﹣2,m),B(n,﹣1)两点.
x+1的图象交于A(﹣2,m),B(n,﹣1)两点.
(1)求反比例函数的解析式;
(2)连接OA,OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(6,0)的直线y=kx﹣3与直线y=﹣x交于点B,点P从点O出发以每秒1个单位长度的速度向点A匀速运动.
(1)求点B的坐标;
(2)当△OPB是直角三角形时,求点P运动的时间;
(3)当BP平分△OAB的面积时,直线BP与y轴交于点D,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若∠DAC=2∠ABC,AC=BC,四边形ABCD是平行四边形,则∠ABC= ;
(2)如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4.求BD的长;
(3)如图3,若∠ABC=30°,∠ACD=45°,AC=2,B、D之间距离是否有最大值?如有求出最大值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用无刻度的直尺和圆规作出符合要求的图形.(注:不要求写作法,但保留作图痕迹)
(1)如图,已知线段AB,作一个△ABC,使得∠ACB=90°;(只需画一个即可)
(2)如图,已知线段MN,作一个△MPN,使得∠MPN=90°且sinM=![]() .(只需画一个即可)
.(只需画一个即可)

(1) (2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国庆节社会实践活动中,盐城某校甲、乙、丙三位同学一起调查了高峰时段盐靖高速、盐洛高速和沈海高速的车流量(每小时通过观测点的汽车车辆数),三位同学汇报高峰时段的车流量情况如下:
甲同学说:“盐靖高速车流量为每小时2000辆.”
乙同学说:“沈海高速的车流量比盐洛高速的车流量每小时多400辆.”
丙同学说:“盐洛高速车流量的5倍与沈海高速车流量的差是盐靖高速车流量的2倍.”
请你根据他们所提供的信息,求出高峰时段盐洛高速和沈海高速的车流量分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC;
②若半圆O的半径为12,求阴影部分的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是常见的工具“人字梯”,量得“人字梯”的一侧OC=OD=2.5米,
(1)若CD=1.4米,求梯子顶端O离地面的高度;

(2)《建筑施工高处作业安全技术规范》规定:使用“人字梯”时,上部夹角(∠AOB)以35°~45°为宜,铰链必须牢固,并应有可靠的拉撑措施.如图,小明在人字梯的一侧A、B处系上一根绳子确保用梯安全,他测得OA=OB=2米,在A、B处打结各需要0.4米的绳子,请你帮小明计算一下,他需要的绳子的长度应该在什么范围内.(结果精确到0.1米,参考数据:sin17.5°≈0.30,cos17.5°≈0.95,tan17. °5≈0.32,sin22.5°≈0.38,cos22.5°≈0.92,tan22.5°≈0.41)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com