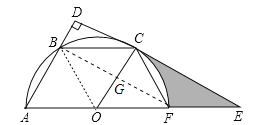
【题目】如图，已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上，过点C作CD⊥AB，分别交AB、AO的延长线于点D、E，AE交半圆O于点F，连接CF．

（1）判断直线DE与半圆O的位置关系，并说明理由；

（2）①求证：CF=OC；

②若半圆O的半径为12，求阴影部分的周长．

参考答案：

【答案】（1）DE是⊙O的切线；（2）①证明见解析；②4π+12+．

【解析】试题分析：（1）结论：DE是⊙O的切线．首先证明△ABO，△BCO都是等边三角形，再证明四边形BDCG是矩形，即可解决问题；

（2）①只要证明△OCF是等边三角形即可解决问题；

②求出EC、EF、弧长CF即可解决问题．

试题解析：（1）结论：DE是⊙O的切线．

理由：∵四边形OABC是平行四边形，又∵OA=OC，∴四边形OABC是菱形，

∴OA=OB=AB=OC=BC，∴△ABO，△BCO都是等边三角形，∴∠AOB=∠BOC=∠COF=60°，

∵OB=OF，∴OG⊥BF，

∵AF是直径，CD⊥AD，∴∠ABF=∠DBG=∠D=∠BGC=90°，∴四边形BDCG是矩形，

∴∠OCD=90°，∴DE是⊙O的切线；

（2）①由（1）可知：∠COF=60°，OC=OF，∴△OCF是等边三角形，∴CF=OC；

②在Rt△OCE中，∵OC=12，∠COE=60°，∠OCE=90°，

∴OE=2OC=24，EC=，

∵OF=12，∴EF=12，∴的长= =4π，

∴阴影部分的周长为4π+12+．

关闭