
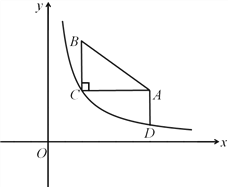
【题目】如图,在平面直角坐标系中,已知Rt△ABC中,∠C=90°,AC=4,BC=3,点A(6,5),B(2,8),反比例函数y![]() 过点C,过点A作AD∥y轴交双曲线于点D.
过点C,过点A作AD∥y轴交双曲线于点D.
(1)求反比例函数y![]() 的解析式;
的解析式;
(2)动点P在y轴正半轴运动,当线段PC与线段PD的差最大时,求P点的坐标;
(3)将Rt△ABC沿直线CO方向平移,使点C移动到点O,求线段AB扫过的面积.
【答案】(1)y=![]() (x>0);(2)26.
(x>0);(2)26.
【解析】分析:(1)根据平行关系确定出C的坐标,然后利用待定系数法求出函数的解析式,并根据图像表示出取值范围;
(2)根据题意判断出:当P、C、D三点共线时,线段PC与线段PD的差最大,求出D点的坐标,利用待定系数法,由C、D的坐标求解即可;
(3)根据平移的性质得到对应点的位置,利用分割法求出图形的面积即可.
详解:(1)设C(x,y)
由于AC∥x轴,BC∥x轴
得x=2,y=5即 C(2.5)
将C点代入y=![]() 得 k=10
得 k=10
则反比例函数为 y=![]() (x>0)
(x>0)
(2)当P、C、D三点共线时,线段PC与线段PD的差最大
设 D(6,a)
代入y=![]() 得a=
得a=![]() 所以D(6,
所以D(6,![]() )
)
设直线CD为y=kx+b, P(0,c)
将C(2.5),D(6,![]() )带入得
)带入得
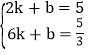
解得: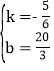
∴y=-![]() x+
x+![]()
将P(0,c)代入得c=![]()
即P(0,![]() )
)
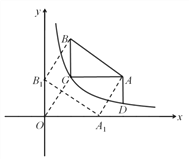
(3)如图所示
由题意可得点C移到点O;点B移到点B1(0,3);点A移到点A1 (4,0)
∴四边形B B1 OC,四边形A A1 OC与四边形B B1 A1 A都是平行四边形
在五边形B B1 OA1 A中有
S△ABC + SB B1 OC + SA A1 OC = S△O B1 A1 + SB B1 A1 A
∴![]() ×3×4+3×2+4×5 =
×3×4+3×2+4×5 =![]() ×3×4 + SB B1 A1 A
×3×4 + SB B1 A1 A
SB B1 A1 A = 26
即线段AB扫过的面积为26.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.例如:1423,
,那么称这个四位数为“和平数”.例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是_________________,最大的“和平数”是_______________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题.
(1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为 ;
(2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点);
(3)人们发现,记格点多边形(顶点均为格点)内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.试确定m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有四个点A,B,C,D.
(1)根据下列语句画图:
①画射线BA;连接BD;
②画直线AD、BC相交于点E;
③在线段DC的延长线上取一点F,使CF=BC,连接EF;
(2)点B与直线AD的关系是 ;
(3)图中以E为顶点的角中,小于平角的角共有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数 yl= x ( x ≥0 ) , ![]() ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3 ![]() 时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8
④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.从纸箱中任意摸出一球,摸到红色球、黄色球的概率分别是0.2、0.3.
(1)试求出纸箱中蓝色球的个数;
(2)小明向纸箱中再放进红色球若干个,小丽为了估计放入的红球的个数,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到红球的频率在0.5附近波动,请据此估计小明放入的红球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
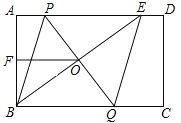
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com