
【题目】如图,矩形![]() 的对角线相交于点
的对角线相交于点![]() ,
,![]() ,
,![]() .
.
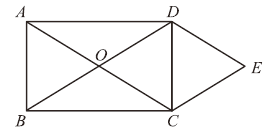
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,
,![]() 的长为
的长为![]() ,求四边形
,求四边形![]() 的周长.
的周长.
【答案】(1)见解析;(2)四边形OCED的周长为16cm.
【解析】
(1)先判定四边形OCED是平行四边形,再根据矩形的对角线相等且互相平分可得OC=OD,然后根据邻边相等的平行四边形是菱形即可得证;
(2)根据矩形的性质,先判定出△AOB是等边三角形,再根据等边三角形的性质求出OA=OB=OC=AB并利用勾股定理求出AB的长度,再根据菱形的面积公式进行计算即可得解.
(1)证明:∵DE∥AC ,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴ AC=BD,
∴OC=OD,
∴四边形OCED是菱形.
(2)解:∵四边形ABCD是矩形,
∴∠ABC= 90°.
∴AC=BD.
∴OA=OB=OC
又∵∠CAB=60,
∴△AOB是等边三角形
∴OA=OB=OC=AB
设AB=x,
∴AC= 2x,
∴![]()
∴![]() ,
,![]() (舍)
(舍)
∴OC=4,
由(1)可知四边形OCED是菱形,故它的周长为16cm.


科目:初中数学 来源: 题型:
【题目】如图,![]() ∥
∥![]() ,BE∥CF,BA⊥
,BE∥CF,BA⊥![]() ,DC⊥
,DC⊥![]() ,下面给出四个结论:①BE=CF;②AB=DC;③
,下面给出四个结论:①BE=CF;②AB=DC;③![]() ;
;
④四边形ABCD是矩形.其中说法正确的有( )
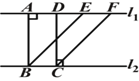
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
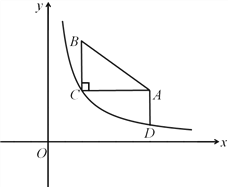
【题目】如图,在平面直角坐标系中,已知Rt△ABC中,∠C=90°,AC=4,BC=3,点A(6,5),B(2,8),反比例函数y![]() 过点C,过点A作AD∥y轴交双曲线于点D.
过点C,过点A作AD∥y轴交双曲线于点D.
(1)求反比例函数y![]() 的解析式;
的解析式;
(2)动点P在y轴正半轴运动,当线段PC与线段PD的差最大时,求P点的坐标;
(3)将Rt△ABC沿直线CO方向平移,使点C移动到点O,求线段AB扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
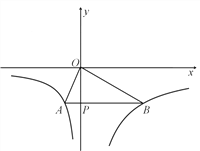
【题目】已知函数的y1=![]() (x<0),y2=
(x<0),y2=![]() (x>0)图象如图所示,点P 是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.当点P移动到使∠AOB=90°时,点P的坐标为________________.
(x>0)图象如图所示,点P 是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.当点P移动到使∠AOB=90°时,点P的坐标为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某一城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天;若由甲队先做20天,剩下的工程由甲、乙两队合做完成.
(1)甲、乙两队合作多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,上下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为多少?(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.236)( )
≈2.236)( )

A. 320cm B. 395.24 cm C. 431.76 cm D. 480 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学捐资购买了一批物资240吨打算扶贫山区。现有甲、乙、丙三种车型可供选择,每辆车的运载能力和运费如下表所示(每辆车均装满)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨) | 10 | 16 | 20 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元。求甲、乙两种车型各多少辆?
(2)为了节约运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知三种车辆总数为14辆。请求出三种车型分别是多少辆?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
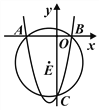
【题目】如图,二次函数y=x2-2mx+8m的图象与x轴交于A、B两点(点A在点B的左边且OA≠OB),交y轴于点C,且经过点(m,9m),⊙E过A、B、C三点。
(1)求这条抛物线的解析式;
(2)求点E的坐标;
(3)过抛物线上一点P(点P不与B、C重合)作PQ⊥x轴于点Q,是否存在这样的点P使△PBQ和△BOC相似?如果存在,求出点P的坐标;如果不存在,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
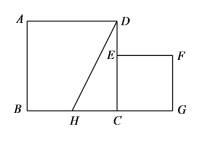
【题目】如图,已知正方形ABCD的边长为1,正方形CEFG的面积为![]() ,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为
,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为![]() ,且
,且![]() .
.
⑴求线段CE的长;
⑵若点H为BC边的中点,连结HD,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com