
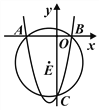
【题目】如图,二次函数y=x2-2mx+8m的图象与x轴交于A、B两点(点A在点B的左边且OA≠OB),交y轴于点C,且经过点(m,9m),⊙E过A、B、C三点。
(1)求这条抛物线的解析式;
(2)求点E的坐标;
(3)过抛物线上一点P(点P不与B、C重合)作PQ⊥x轴于点Q,是否存在这样的点P使△PBQ和△BOC相似?如果存在,求出点P的坐标;如果不存在,说明理由
【答案】(1)y=x2+2x-8(2)(-1,-![]() )(3)(-8,40),(-
)(3)(-8,40),(-![]() ,-
,-![]() ),(-
),(-![]() ,-
,-![]() )
)
【解析】分析:(1)把![]() 代入解析式,得:
代入解析式,得:![]() ,解这个方程可求出m的值;
,解这个方程可求出m的值;
(2)分别令y=0和x=0,求出OA,OB,OC及AB的长,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() ,AE,设OF=GE=a,根据
,AE,设OF=GE=a,根据![]() ,列方过程求出a的值,从而求出点E的坐标;
,列方过程求出a的值,从而求出点E的坐标;
(3)设点P(a, a2+2a-8), 则![]() ,然后分
,然后分![]() ∽
∽![]() 时和
时和![]() ∽
∽![]() 时两种情况,列比例式求出a的值,从而求出点P的坐标.
时两种情况,列比例式求出a的值,从而求出点P的坐标.
详解:(1)把![]() 代入解析式,得:
代入解析式,得:![]()
解得:![]() (舍去)
(舍去)
∴![]()
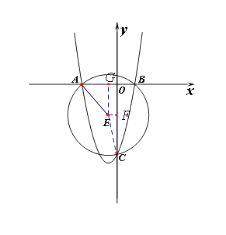
(2)由(1)可得:![]() ,当
,当![]() 时,
时,![]() ;
;
∵点A在点B的左边 ∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]()
过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() ,
,
则![]() ,
,
![]()
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(3)设点![]() ,
,
则![]() ,
,
a.当![]() ∽
∽![]() 时,
时,
![]() ,即
,即![]() ,
,
解得:![]() (舍去);
(舍去);
![]() (舍去);
(舍去);![]() ,
,
∴![]() ;
;
b.当![]() ∽
∽![]() 时,
时,
![]() ,即
,即![]() ,
,
解得:![]() (舍去),
(舍去),![]() ;
;![]() ,
,
∴![]() ;
;![]() ;
;
综上所述,点![]() 的坐标为:
的坐标为:![]() ,
,![]() ,
,![]()


科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
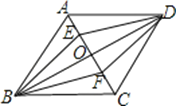
【题目】如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③△DEF是轴对称图形;④∠ADE=∠EDO;⑤四边形ABCD面积为EF×BD.其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳某工厂从美国进口A、B两种产品销售,已知每台A种产品进价为3000元,售价为4800元;受中美贸易大战的影响,每台B种产品的进价上涨500元,进口相同数量的B种产品,在中美贸易大战开始之前只需要60万元,中美贸易大战开始之后需要80万元。
(1)中美贸易大战开始之后,每台B种产品的进价为多少?
(2)中美贸易大战开始之后,如果A种产品的进价和售价不变,每台B种产品在进价的基础上提高40%作为售价。公司筹集到不多于35万元且不少于33万元的资金用于进口A、B两种产品共150台,请你设计一种进货方案使销售后的总利润最大。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
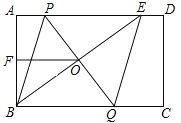
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案;在甲超市累计购买商品超出200元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出100元之后,超出部分按原价8.5折优惠,设顾客购物的原费用是x元(x>200).
(1)请用含x的代数式分别表示顾客在两家超市购物所付的实际费用;
(2)李明慧准备购买300元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明慧购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学科代表小芳对本年级同学参加课外兴趣小组活动情况进行随机抽样调查,根据调查数据小芳同学还制作了参加课外兴趣小组活动情况的两个统计图(见下图)
(1)此次被调查的人数是多少?
(2)将图②补充完整;
(3)求出图①中表示“写作”兴趣小组的扇形圆心角度数;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com