
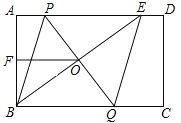
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
【答案】(1)证明见解析;(2)PQ的长是![]() .
.
【解析】试题分析:⑴先根据线段垂直平分线的性质证明QB=QE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形ABGE是平行四边形,再根据菱形的判定即可得出结论.
⑵根据三角形中位线的性质可得![]() ,设
,设![]() ,则
,则
![]() ,在Rt△ABE中,根据勾股定理可得
,在Rt△ABE中,根据勾股定理可得![]() ,解得BE=10,
,解得BE=10,
得到![]() ,设
,设![]() ,则
,则![]() ,
, ![]() ,计算得出
,计算得出![]() ,在Rt△BOP中,根据勾股定理可得
,在Rt△BOP中,根据勾股定理可得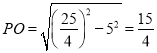 ,由
,由![]() 即可求解.
即可求解.
试题解析:
(1)证明:∵ PQ垂直平分BE,
∴ QB=QE,OB=OE,
∵ 四边形ABCD是矩形,
∴ AD∥BC,
∴ ∠ PEO=∠ QBO,
在△ BOQ与△ EOP中,
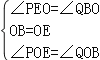 ,
,
∴ △ BOQ≌ △ EOP(ASA),
∴ PE=QB,
又∵ AD∥BC,
∴ 四边形BPEQ是平行四边形,
又∵ QB=QE,
∴ 四边形BPEQ是菱形;
(2)解:∵ O,F分别为PQ,AB的中点,
∴ AE+BE=2OF+2OB=18,
设AE=x,则BE=18﹣x,
在Rt△ ABE中,62+x2=(18﹣x)2,
解得x=8,
BE=18﹣x=10,
∴ OB=![]() BE=5,
BE=5,
设PE=y,则AP=8﹣y,BP=PE=y,
在Rt△ ABP中,62+(8﹣y)2=y2,解得y=![]() ,
,
在Rt△ BOP中,PO=![]() =
=![]() ,
,
∴ PQ=2PO=![]() .
.


科目:初中数学 来源: 题型:
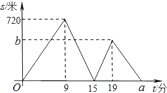
【题目】甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达科技馆;②乙的速度是甲速度的2.5倍;③b=460;④a=25.其中正确的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
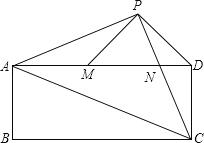
【题目】已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
(1)若AP=![]() ,AB=
,AB=![]() BC,求矩形ABCD的面积;
BC,求矩形ABCD的面积;
(2)若CD=PM,求证:AC=AP+PN.
查看答案和解析>>
科目:初中数学 来源: 题型:
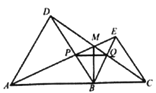
【题目】如图,点A,B,C在同一直线上,在这条直线同侧作等边△ABD和等边△BCE,连接AE和CD,交点为M,AE交BD于点P,CD交BE于点Q,连接PQ、BM, 有4个结论:①△ABE≌△DBC,②△DQB≌△ABP,③∠EAC=30°,④∠AMC=120°,请将所有正确结论的序号填在横线上______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.

(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下问题,不适合用全面调查的是( )
A.了解全班同学每周体育锻炼的时间B.鞋厂检查生产的鞋底能承受的弯折次数
C.学校招聘教师,对应聘人员面试D.某中学调查全校753名学生的身高
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com