
【题目】如图,上下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为多少?(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.236)( )
≈2.236)( )

A. 320cm B. 395.24 cm C. 431.76 cm D. 480 cm
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数 yl= x ( x ≥0 ) , ![]() ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3 ![]() 时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8
④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在艺术节中组织中小学校文艺汇演,甲、乙两所学校共92名学生![]() 其中甲校学生多于乙校学生,且甲校学生不足90名
其中甲校学生多于乙校学生,且甲校学生不足90名![]() ,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两所学校单独购买服装,一共应付5000元
(1)甲、乙两校各有多少名学生准备参加汇演?
(2)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(3)如果甲校有10名学生被调去参加书法绘画比赛不能参加演出,请你为两校设计购买服装方案,并说明哪一种最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,记
中,记![]() 与
与![]() 的函数
的函数![]() (
(![]() ≠0,n≠0)的图象为图形G, 已知图形G与
≠0,n≠0)的图象为图形G, 已知图形G与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,函数
时,函数![]() 有最小(或最大)值n, 点B的坐标为(
有最小(或最大)值n, 点B的坐标为(![]() ,
, ![]() ),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.
),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.

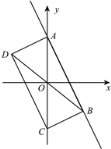
(1)如图,若函数![]() 的图象记为图形G,求图形G的伴随直线的表达式;
的图象记为图形G,求图形G的伴随直线的表达式;
(2)如图,若图形G的伴随直线的表达式是![]() ,且伴随四边形的面积为12,求
,且伴随四边形的面积为12,求![]() 与
与![]() 的函数
的函数![]() (m>0,n <0)的表达式;
(m>0,n <0)的表达式;
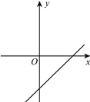
(3)如图,若图形G的伴随直线是![]() ,且伴随四边形ABCD是矩形,求点B的坐标.
,且伴随四边形ABCD是矩形,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③△DEF是轴对称图形;④∠ADE=∠EDO;⑤四边形ABCD面积为EF×BD.其中正确的结论有( )
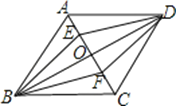
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解决问题:
(1)数学课上,老师提出如下问题:
观察下列算式:
![]() ;
;
![]() ;
;
![]()
![]()
![]()
…
若字母![]() 表示自然数,用含
表示自然数,用含![]() 的式子表示观察得到的规律是
的式子表示观察得到的规律是![]() ;
;
(2)小云同学解决完老师提出的问题后,又继续研究,发现:
①当![]() 表示负整数且
表示负整数且![]() 时,上述规律仍旧成立;
时,上述规律仍旧成立;
②当![]() 表示分数且
表示分数且![]() 时,上述规律仍旧成立.
时,上述规律仍旧成立.
请你对小云的两个发现进行验证,每个发现举出一个算式;
(3)请你参照小云同学的研究思路,进行猜想,验证、归纳,当![]() 时,
时,![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(4)进一步进行猜想、验证、归纳,当![]() (
(![]() 为有理数)时,
为有理数)时,![]() (用含
(用含![]() ,
,![]() ,
,![]() 的代数式表示)。
的代数式表示)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com