
����Ŀ��ij��������������֯��СѧУ���ջ��ݣ��ס�������ѧУ��92��ѧ��![]() ���м�Уѧ��������Уѧ�����Ҽ�Уѧ������90��
���м�Уѧ��������Уѧ�����Ҽ�Уѧ������90��![]() ������ͳһ�����װ�μ��ݳ����±���ij��װ���������ݳ���װ�۸����
������ͳһ�����װ�μ��ݳ����±���ij��װ���������ݳ���װ�۸����
�����װ������ | 1����45�� | 46����90�� | 91������ |
ÿ��װ�ļ۸� | 60Ԫ | 50Ԫ | 40Ԫ |
�������ѧУ���������װ��һ��Ӧ��5000Ԫ
��1���ס�����У���ж�����ѧ�����μӻ��ݣ�
��2������ס�����У�������������װ����ô�ȸ��Թ����װ�����Խ�ʡ����Ǯ��
��3�������У��10��ѧ������ȥ�μ��鷨�滭�������ܲμ��ݳ�������Ϊ��У��ƹ����װ��������˵����һ����ʡǮ��
���𰸡�![]() ��У��52��ѧ�����μ��ݳ�����У��40��ѧ�����μ��ݳ���
��У��52��ѧ�����μ��ݳ�����У��40��ѧ�����μ��ݳ���![]() �ס�����У�������������װ�ȸ��Թ����װ�����Խ�ʡ1320Ԫ��
�ס�����У�������������װ�ȸ��Թ����װ�����Խ�ʡ1320Ԫ��![]() ����У���Ϲ����װ����Ҫ
����У���Ϲ����װ����Ҫ![]() Ԫ��
Ԫ��![]() ����У���Թ����װ����Ҫ
����У���Թ����װ����Ҫ![]() Ԫ��
Ԫ��![]() ����У���Ϲ���91��װ����Ҫ
����У���Ϲ���91��װ����Ҫ![]() Ԫ����ʡǮ�Ĺ����װ��������У���Ϲ���91��װ��
Ԫ����ʡǮ�Ĺ����װ��������У���Ϲ���91��װ��
��������
��1�����У��x��ѧ���μ��ݳ�������У�У�92-x����ѧ���μ��ݳ��������ܼ�![]() ����
����![]() �����������һ��Ӧ��5000Ԫ���ó�����x��һԪһ�η��̣��ⷽ�̵ó����ۣ�
�����������һ��Ӧ��5000Ԫ���ó�����x��һԪһ�η��̣��ⷽ�̵ó����ۣ�
��2����5000 - 92��װ������ã�����������ۣ�
��3��������Թ����װ��һ������91��װ������ã��ȽϺɵó����ۣ�
�⣺![]() ���У��x��ѧ�����μ��ݳ�������У��
���У��x��ѧ�����μ��ݳ�������У��![]() ��ѧ���μ��ݳ���
��ѧ���μ��ݳ���
��������ã�![]()
��ã�![]() ��
��
![]() ��
��
�𣺼�У��52��ѧ�����μ��ݳ�����У��40��ѧ�����μ��ݳ���
![]() ������ã�
������ã�![]() Ԫ
Ԫ![]() ��
��
�𣺼ס�����У�������������װ�ȸ��Թ����װ�����Խ�ʡ1320Ԫ��
![]() ��Ϊ��У��10��ѧ�����ܲμ��ݳ������У��42��ѧ���μ��ݳ���
��Ϊ��У��10��ѧ�����ܲμ��ݳ������У��42��ѧ���μ��ݳ���
![]() ����У���Ϲ����װ������Ҫ
����У���Ϲ����װ������Ҫ![]()
![]() Ԫ
Ԫ![]() ��
��
![]() ����У���Թ����װ������Ҫ
����У���Թ����װ������Ҫ![]() Ԫ
Ԫ![]()
![]() ����У���Ϲ���91��װ������Ҫ
����У���Ϲ���91��װ������Ҫ![]()
![]() Ԫ
Ԫ![]()
������������ʡǮ�Ĺ����װ��������У���Ϲ���91��װ��
�ʴ�Ϊ����1����У��52��ѧ�����μ��ݳ�����У��40��ѧ�����μ��ݳ�����2���ס�����У�������������װ�ȸ��Թ����װ�����Խ�ʡ1320Ԫ����3��![]() ����У���Ϲ����װ����Ҫ4100Ԫ��
����У���Ϲ����װ����Ҫ4100Ԫ��![]() ����У���Թ����װ����Ҫ4920Ԫ��
����У���Թ����װ����Ҫ4920Ԫ��![]() ����У���Ϲ���91��װ����Ҫ3640Ԫ����ʡǮ�Ĺ����װ��������У���Ϲ���91��װ��
����У���Ϲ���91��װ����Ҫ3640Ԫ����ʡǮ�Ĺ����װ��������У���Ϲ���91��װ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ĵ����ϣ�10����ȫ��ͬ���ⳤΪ8cm��С������ѳ�һ�������壮
��1��������������л��������濴�ʹ����濴����״ͼ��
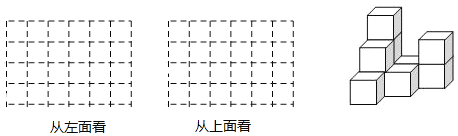
��2����������������ı��棨�������棩���ϻ�ɫ���ᣬ��������������������Ƕ���cm2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ֵ���ʶ�������ٰ��ˡ�������д����������ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱ��д50�����֣���ÿ��ȷ��д��һ�����ֵ�1�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 25��x��30 | 4 |
��2�� | 30��x��35 | 6 |
��3�� | 35��x��40 | 14 |
��4�� | 40��x��45 | a |
��5�� | 45��x��50 | 10 |
����ͼ��������и��⣺
��1�������a��ֵ��
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�������Գɼ�������40��Ϊ���㣬�β��Ե��������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�죬ij����Ѳ�߳��ڶ������������·��Ѳ�ߣ����Ӹ�ͤ![]() ����������ͣ����
����������ͣ����![]() ��.�涨����Ϊ������������Ϊ����������ʻ�����¼���£���λ��ǧ�ף���
��.�涨����Ϊ������������Ϊ����������ʻ�����¼���£���λ��ǧ�ף���
+5��-8��+10��-12��+6��-18��+5��-2.
��1��![]() ���ڸ�ͤ
���ڸ�ͤ![]() ��ʲô�������ͤ
��ʲô�������ͤ![]() ��Զ��
��Զ��
��2����Ѳ�߳�ÿ��ʻ1ǧ����0.1������һ�칲���Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c��Ϊʵ������a>b��c��0�����н��۲�һ����ȷ����
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Լ1�ȵ磬���Լ���0.785ǧ��̼�ŷţ�ijʡ��2018��6��1����ִ���µľ��������õ�۸�һ��һ�������û���ʵʩ����ʽ�۽���ۣ����õ�������50ǧ��ʱ(��50ǧ��ʱ)���ֲ����������ÿǧ��ʱ0.53Ԫ�����õ�����51��200ǧ��ʱ���֣����ÿǧ��ʱ�ϵ�0.03Ԫ�����õ�������200ǧ��ʱ���֣����ÿǧ��ʱ�ϵ�0.10Ԫ��
С������һ��һ�������û�����ʵʩ����ʽ�۽����.7�·���8�·ݵĵ�ѽɿ�������±���
�������� | ����ʾ�� | ����ʾ�� | ���� | ���(Ԫ) |
20180710 | 3 230 | 3 296 | 66 | 34.98 |
20180810 | 3 296 | 3 535 | 239 | 135.07 |
(1)�����������϶Խ���ʽ�۽���۵������������Ϊxǧ��ʱ�����ΪyԪ����ʾ�������ڵ����ĺ�����ϵ��������ͼ��
(2)����С����8�·ݵ�ѵļ������飮
(3)Ϊ��Լ�õ磬С�����Ժ��ƶ�����ϸ���õ�ƻ������ʵ��ÿ��ȼƻ�����2ǧ��ʱ�������õ������ᳬ��240ǧ��ʱ�����ʵ��ÿ��ȼƻ���Լ2ǧ��ʱ����ô�����õ����������180ǧ��ʱ������(30��)ÿ���õ���Ӧ������ʲô��Χ�ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У������P��x��y���ı任��ΪP�䣨x+y��x��y����
��1����ͼ1��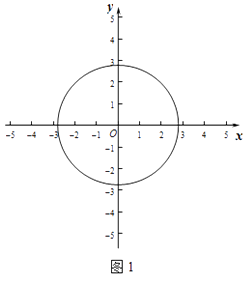
�����O�İ뾶Ϊ ![]() ��
��
�������ж�M��2��0����N����2����1��������ı任�����O��λ�ù�ϵ��
������P��ֱ��y=x+2�ϣ���P�ı任��P���ڡ�O���ڣ����P�������ȡֵ��Χ��
��2����ͼ2�������O�İ뾶Ϊ1����P�ı任��P����ֱ��y=��2x+6�ϣ����P���O������һ��������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���߳���������������������γ�Ϊ�����������Ρ�.
��ѧѧϰС���ͬѧ��32���ȳ��Ļ�����ÿ�����ȼ�Ϊ1����λ����ȡ�����ɸ�����β���������������Σ�����̽���.
С����12���������ڳ���ͼ��ʾ�ġ����������Ρ���
Сӱ�ֱ���24����30�������ڳ�ֱ�ǡ����������Ρ���
С���ܵ�С����Сӱ���������ֱ�ڳ�������ͬ�ĵ��������������Ρ�.

�����㻭��Сӱ��С�ڳ��ġ����������Ρ���ʾ��ͼ��
�����ܷ�Ҳ����ȡ�����ɸ���������Ҫ��ڳ������������Ρ�������ܣ��뻭��ʾ��ͼ��������ܣ���˵������.
�ٻ����ȱߡ����������Ρ���
�ڰڳ�һ�������⣨�ȷ�ֱ�������Σ�Ҳ�ǵ��������Σ������������Ρ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ط��������������50km��A��B��վ֮��Ĺ�·��E�㣬��һ�����ز��ӹ����أ���ʹC��D���嵽E��ľ�����ȣ���֪DA��AB��A��CB��AB��B��DA=30km��CB=20km����ô����EӦ������Aվ����ǧ�ĵط���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com