
【题目】节约1度电,可以减少0.785千克碳排放.某省从2018年6月1日起执行新的居民生活用电价格,一户一表居民用户将实施阶梯式累进电价:月用电量低于50千瓦时(含50千瓦时)部分不调整,电价每千瓦时0.53元;月用电量在51~200千瓦时部分,电价每千瓦时上调0.03元;月用电量超过200千瓦时部分,电价每千瓦时上调0.10元.
小明家属一户一表居民用户,将实施阶梯式累进电价.7月份至8月份的电费缴款情况如下表:
计算日期 | 上期示度 | 本期示度 | 电量 | 金额(元) |
20180710 | 3 230 | 3 296 | 66 | 34.98 |
20180810 | 3 296 | 3 535 | 239 | 135.07 |
(1)根据上述资料对阶梯式累进电价的描述,设电量为x千瓦时,金额为y元,表示出金额对于电量的函数关系,并画出图象.
(2)解释小明家8月份电费的计算详情.
(3)为节约用电,小明对以后制订了详细的用电计划,如果实际每天比计划多用2千瓦时,下月用电量将会超过240千瓦时;如果实际每天比计划节约2千瓦时,那么下月用电量将会不超过180千瓦时,下月(30天)每天用电量应控制在什么范围内?
【答案】(1)见解析;(2)见解析;(3)下月每天用电量应控制在大于6千瓦时小于或等于8千瓦时范围内.
【解析】
(1)读懂题意,列式得出关系式,进而画出图象;
(2)读懂题意,进而解释小明家8月份电费的计算详情即可;
(3)设下月小明家的用电量是x千瓦时,根据题意求解即可.
(1)阶梯式累进电价的数学模型可用分段函数表示,设电量为x千瓦时,金额为y元,则有y=
即y=
函数图象如下图所示:

(2)基本部分:239×0.53=126.67(元);
调价部分:50~200千瓦时之间调价部分:(200-50)×0.03=4.5(元);
超过200千瓦时的调价部分:(239-200)×0.10=3.9(元);
合计调价部分电费:4.5+3.9=8.4(元);
合计电费:126.67+8.4=135.07(元).
(3)设下月每天用电量为x,根据题意列不等式组,得
![]() 解之,得6<x≤8.
解之,得6<x≤8.
所以下月每天用电量应控制在大于6千瓦时小于或等于8千瓦时范围内.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小刚在实践课上要做一个如图1所示的折扇,折扇扇面的宽度AB是骨柄长OA的 ![]() ,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为24
,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为24 ![]() cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为( )
cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为( )
A.21cm
B.20 cm
C.19cm
D.18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列四种说法:①小明中途休息用了20分钟;②小明休息前爬山的平均速度为每分钟70米;③小明在上述过程中所走的路程为6600米;④小明休息前爬山的平均速度大于休息后爬山的平均速度.其中正确的是________(填序号).
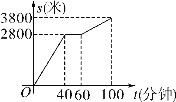
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究:哪些特殊的角可以用一副三角板画出?
在①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
(2)在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种.如图,他先用三角板画出了直线![]() ,然后将一副三角板拼接在一起,其中
,然后将一副三角板拼接在一起,其中![]() 角(
角(![]() )的顶点与
)的顶点与![]() 角(
角(![]() )的顶点互相重合,且边
)的顶点互相重合,且边![]() 、
、![]() 都在直线
都在直线![]() 上.固定三角板
上.固定三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 按顺时针方向旋转一个角度
按顺时针方向旋转一个角度![]() ,当边
,当边![]() 与射线
与射线![]() 第一次重合时停止.
第一次重合时停止.

①当![]() 平分
平分![]() 时,求旋转角度
时,求旋转角度![]() ;
;
②是否存在![]() ?若存在,求旋转角度
?若存在,求旋转角度![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在艺术节中组织中小学校文艺汇演,甲、乙两所学校共92名学生![]() 其中甲校学生多于乙校学生,且甲校学生不足90名
其中甲校学生多于乙校学生,且甲校学生不足90名![]() ,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两所学校单独购买服装,一共应付5000元
(1)甲、乙两校各有多少名学生准备参加汇演?
(2)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(3)如果甲校有10名学生被调去参加书法绘画比赛不能参加演出,请你为两校设计购买服装方案,并说明哪一种最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1……如此作下去,若OA=OB=1.
(1)A1B=________,S△A1B1A2=________;
(2)试猜想第n个等腰直角三角形的面积Sn.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了m,恰好把水喷到F处进行灭火.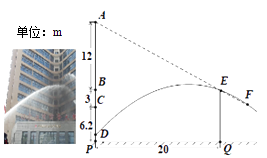
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com