Question

【题目】在平面直角坐标系xOy中，定义点P（x，y）的变换点为P′（x+y，x﹣y）．
（1）如图1，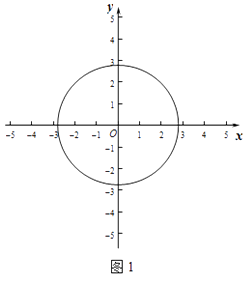

如果⊙O的半径为 ，
①请你判断M（2，0），N（﹣2，﹣1）两个点的变换点与⊙O的位置关系；
②若点P在直线y=x+2上，点P的变换点P′在⊙O的内，求点P横坐标的取值范围．
（2）如图2，如果⊙O的半径为1，且P的变换点P′在直线y=﹣2x+6上，求点P与⊙O上任意一点距离的最小值．

Answer 1

【答案】
（1）解：①M（2，0）的变换点M′的坐标为（2，2），则OM′= =2 ，所以点M（2，0）的变换点在⊙O上；

N（﹣2，﹣1）的变换点N′的坐标为（﹣3，﹣1），则ON′= = ＞2 ，所以点N（﹣2，﹣1）的变换点在⊙O外；

②设P点坐标为（x，x+2），则P点的变换点为P′的坐标为（2x+2，﹣2），则OP′= ，

∵点P′在⊙O的内，

∴ ＜2 ，

∴（2x+2）2＜4，即（x+1）2＜1，

∴﹣1＜x+1＜1，解得﹣2＜x＜0，

即点P横坐标的取值范围为﹣2＜x＜0；

（2）解：设点P′的坐标为（x，﹣2x+6），P（m，n），

根据题意得m+n=x，m﹣n=﹣2x+6，

∴3m+n=6，

即n=﹣3m+6，

∴P点坐标为（m，﹣3m+6），

∴点P在直线y=﹣3x+6上，

设直线y=﹣3x+6与x轴相交于点A，与y轴相交于点B，过O点作OH⊥AB于H，交⊙O于C，如图2，

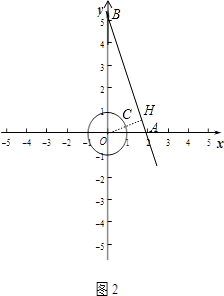
则A（2，0），B（0，6），

∴AB= =2 ，

∵ OHAB= OAOB，

∴OH= = ，

∴CH= ﹣1，

即点P与⊙O上任意一点距离的最小值为 ﹣1．

【解析】（1）比较d与r的大小可以判定点与圆的位置关系；（2）利用变换法则，求出变换点P'的运动轨迹为直线，圆上的点与直线的最短距离可转化为圆心到直线的距离减去半径.