
【题目】(1)动手操作:
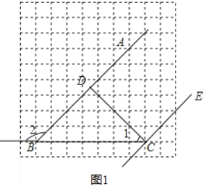
如图1所示,已知A、B、C三个点都在网格纸的格点上,∠1是∠ABC的余角,∠2是∠ABC的补角,CD⊥AB于点D,CE∥AB,试在图中分别画出:∠1、∠2、垂线段CD和直线CE.
(2)已知:如图2,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D,试说明:AC∥DF,请将下面的解答过程补充完整:
解:∵∠1=∠2(已知)
又∵∠1=∠3
∴ = (等量代换)
∴EC∥DB
∴∠C= (两直线平行,同位角相等)
∵∠C=∠D(已知)
∴∠D=
∴AC∥DF

【答案】(1)画图见解析;(2)对顶角相等,∠2=∠3,同位角相等两直线平行,∠ABD,∠ABD,内错角相等两直线平行
【解析】
(1)根据垂线段、平行线的判定,余角,补角的定义画出图形即可;
(2)只要证明∠D=∠ABD,即可解决问题
(1)∠1、∠2、垂线段CD和直线CE如图所示:
(2)∵∠1=∠2(已知)
又∵∠1=∠3(对顶角相等)
∴∠2=∠3(等量代换)
∴EC∥DB(同位角相等,两直线平行)
∴∠C=∠ABD(两直线平行,同位角相等)
∵∠C=∠D(已知)
∴∠D=∠ABD,
∴AC∥DF(内错角相等,两直线平行)
故答案为:对顶角相等,∠2=∠3,同位角相等两直线平行,∠ABD,∠ABD,内错角相等两直线平行;


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,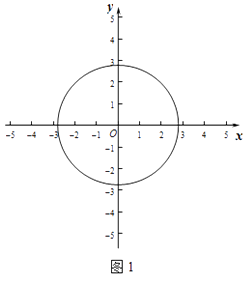
如果⊙O的半径为 ![]() ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如:下问题
尺规作图:过圆外一点作园的切线
已知:圆O和点P
求作:过点P的圆O的切线
小涵的主要作法如下:
如图:①连接OP,作线段OP的中点A
②以A为圆心,OA长为半径作圆,交圆O于点B,C
③作直线PB和PC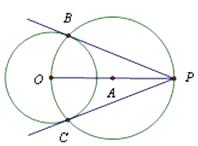
所以PB和PC就是所求的切线
老师说:“小涵的作法正确.”
请回答:小涵的作图依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.

⑴请你画出小颖和小辉摆出的“整数三角形”的示意图;
⑵你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
①画出等边“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线——螺旋前进的.
通过阅读以上信息,解决下列问题:
(1)若树干的周长(即图中圆柱的底面周长)为30cm,葛藤绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少?
(2)若树干的周长为80cm,葛藤绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车上学,某天他从家出发骑行了一段路程,想起要买一本书,于是折回到他刚经过的某书店,买到书后继续去学校.以下是他在本次上学离家的距离与所用的时间的关系示意图,根据图中提供的信息解答下列问题:
(1)小明家与学校的距离是_____米.
(2)小明在书店停留了多少分钟?
(3)从A,B两题中任选一题作答:
A.小明骑行过程中哪个时间段的速度最快,最快的速度是多少?
B.小明在这次上学过程中的平均速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, ![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD, DE,直接写出△BDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com