练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】阅读下面材料：
    在数学课上，老师提出如：下问题
    尺规作图：过圆外一点作园的切线
    已知：圆O和点P

    求作：过点P的圆O的切线
    小涵的主要作法如下：
    如图：①连接OP，作线段OP的中点A
    ②以A为圆心，OA长为半径作圆，交圆O于点B，C
    ③作直线PB和PC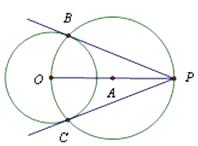

    所以PB和PC就是所求的切线
    老师说：“小涵的作法正确．”
    请回答：小涵的作图依据是 ．

    【答案】到线段两个端点距离相等的点在线段的垂直平分线上,两点确定一条直线．
    【解析】∵CA=CB，DA=DB，

    ∴CD垂直平分AB（到线段两个端点距离相等的点在线段的垂直平分线上，两点确定一条直线．）


    【考点精析】本题主要考查了圆周角定理和切线的判定定理的相关知识点，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】李明上星期买进某公司股票7000股，每股27元，下表为本周每日该股票的涨跌情况单位：元

    星期

    一

    二

    三

    四

    五

    六

    每股涨跌

    这六天中，哪几天的股票是上涨的？哪几天的股票是下跌的？

    哪天股票上涨的最多？你能算出这天收盘时每股是多少元吗？

    本周六收盘时每股是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，、两点在线段上，且，点为的中点.

    （1）判断线段与的大小关系，并说明理由；

    （2）若，求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A处的正上方，如果每次发出的乒乓球的运动路线固定不变，且落在中线上，在乒乓球从发射出到第一次落在桌面的运行过程中，设乒乓球与端点A的水平距离为x（米），距桌面的高度为y（米），运行时间为t（秒），经多次测试后，得到如下部分数据：

    t（秒）

    0

    0.16

    0.2

    0.4

    0.6

    0.64

    0.8

    …

    x（米）

    0

    0.4

    0.5

    1

    1.5

    1.6

    2

    …

    y（米）

    0.25

    0.378

    0.4

    0.45

    0.4

    0.378

    0.25

    …


    （1）如果y是t的函数，
    ①如图，在平面直角坐标系tOy中，描出了上表中y与t各对对应值为坐标的点．请你根据描出的点，画出该函数的图象；

    ②当t为何值时，乒乓球达到最大高度？
    （2）如果y是关于x的二次函数，那么乒乓球第一次落在桌面时，与端点A的水平距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】大家已经知道，完全平方公式和平方差公式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式也可以用这种形式表示，例如：2x（x+y）=2x2+2xy就可以用图的面积表示．

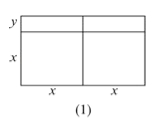
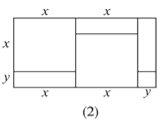
    （1）请写出图（2）所表示的代数恒等式：　_______　；

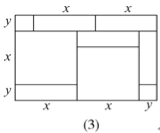
    （2）请写出图（3）所表示的代数恒等式：　________　；

    （3）试画出一个几何图形，使它的面积能表示（x+y）（x+3y）=x2+4xy+3y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）动手操作：

    如图1所示，已知A、B、C三个点都在网格纸的格点上，∠1是∠ABC的余角，∠2是∠ABC的补角，CD⊥AB于点D，CE∥AB，试在图中分别画出：∠1、∠2、垂线段CD和直线CE．

    （2）已知：如图2，点E在DF上，点B在AC上，∠1＝∠2，∠C＝∠D，试说明：AC∥DF，请将下面的解答过程补充完整：

    解：∵∠1＝∠2（已知）

    又∵∠1＝∠3

    ∴ ＝ （等量代换）

    ∴EC∥DB

    ∴∠C＝ （两直线平行，同位角相等）

    ∵∠C＝∠D（已知）

    ∴∠D＝

    ∴AC∥DF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某机动车出发前油箱中有油42升，行驶若干小时后，途中在加油站加油若干升，油箱中余油量Q（L）与行驶时间t（h）之间的函数关系如图所示，根据图回答问题：

    （1）机动车行驶了 小时后加油，加油 升；

    （2）加油后油箱中的油最多可行驶多少小时？

    （3）加油前油箱余油量Q与行驶时间t的函数关系式是 ；

    （4）如果加油站距目的地还有230km，车速为40km/h，要到达目的地，油箱中的油是否够用？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC，AB＝AC＝5，BC＝6，若点P在边AC上移动，则BP的最小值是_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了迎接阜阳九中校园文化艺术节的召开，现要从七、八年级学生中抽调人参加 “校园集体舞”、“广播体操”、“唱红歌”等训练活动，其中参加 “校园集体舞”人数是抽调人数的还多3人，参加“广播体操”活动人数是抽调人数的少2人，其余的参加“唱红歌”活动，若抽调的每个学生只参加了一项活动。

    （1）求参加“唱红歌”活动的人数。（用含的式子表示）

    （2）求参加“广播体操”比参加 “校园集体舞蹈”多的人数。（用含的式子表示）

    （3）求当=84时，参加“广播体操比赛” 的人数.

    查看答案和解析>>

    同步练习册答案