
【题目】函数 yl= x ( x ≥0 ) , ![]() ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3 ![]() 时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8
④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .

【答案】①③④
【解析】逐项分析求解后利用排除法求解.①可列方程组求出交点A的坐标加以论证.②由图象分析论证.③根据已知先确定B、C点的坐标再求出BC.④由已知和函数图象分析.
解:①根据题意列解方程组 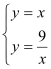 ,
,
解得  ,
, ;
;
∴这两个函数在第一象限内的交点A的坐标为(3,3),正确;
②当x>3时,y1在y2的上方,故y1>y2,错误;
③当x=1时,y1=1,y2==9,即点C的坐标为(1,1),点B的坐标为(1,9),所以BC=9-1=8,正确;
④由于y1=x(x≥0)的图象自左向右呈上升趋势,故y1随x的增大而增大,
y2=![]() (x>0)的图象自左向右呈下降趋势,故y2随x的增大而减小,正确.
(x>0)的图象自左向右呈下降趋势,故y2随x的增大而减小,正确.
因此①③④正确,②错误.
故答案为:①③④.
本题考查了一次函数和反比例函数图象的性质.解决此类问题的关键是由已知和函数图象求出正确答案加以论证.


科目:初中数学 来源: 题型:
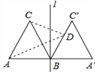
【题目】如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
A. 4 B. 3![]() C. 2
C. 2![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
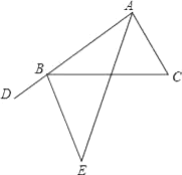
【题目】完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE
(1)求证:∠DBE=∠CBE
证明:∵∠C=∠CBE(已知)
∴BE∥AC________
∴∠DBE=∠DAC________
∵∠DAC=∠C(已知)
∴∠DBE=∠CBE________
(2)请模仿(1)的证明过程,尝试说明∠E=∠BAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图.
请你根据以上的信息,回答下列问题:
(1)本次共调查了名学生,其中最喜爱戏曲的有人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是 .
(2)根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:
①过一点有且只有一条直线与已知直线平行;
②若(t﹣4)2-3t=1,则t可以取的值有3个;
③多项式乘以单项式,积的次数等于多项式的次数与单项式次数的积
④关于x,y的方程组![]() ,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,其中当a每取一个值时,就有一个方程,而这些方程总有一个公共解,则这个公共解是
,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,其中当a每取一个值时,就有一个方程,而这些方程总有一个公共解,则这个公共解是![]() ,其中错误的是( )
,其中错误的是( )
A. ②③④B. ①③④C. ②③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第100个图中共有点的个数是
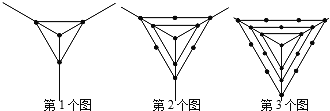
A. 15151B. 15152C. 15153D. 15154
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=ax+b与直线y=x+c的交点的横坐标为1,根据图象有下列四个结论:①a<0;②c>0;③对于直线y=x+c上任意两点A(xA,yA)、B(xB,yB),若xA<xB,则yA>yB;④x>1是不等式ax+b<x+c的解集,其中正确的结论是( )

A. ①②B. ①③C. ①④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有200个零件,平均分给甲、乙两车间加工,由于乙另有任务,所以在甲开始工作2小时后,乙才开始工作,因此比甲迟20分钟完成任务.已知乙每小时加工零件的个数是甲的2倍,问甲、乙两车间每小时各加工多少零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地上年度电价为0.8元,年用电量为1亿度,本年度计划将电价调至0.55﹣0.75之间,经测算,若电价调至x元,则本年度新增用电量y(亿度)与(x﹣0.4)(元)成反比例,又当x=0.65时,y=0.8.根据y与x之间的函数关系式,请你预算,如果每度电的成本价为0.3元,电价调至0.6元时,本年度电力部门的纯收入是_____亿元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com