
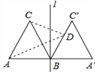
【题目】如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
A. 4 B. 3![]() C. 2
C. 2![]() D. 2+
D. 2+![]()
【答案】A
【解析】连接CC′,连接A′C交y轴于点D,连接AD,此时AD+CD的值最小,根据等边三角形的性质即可得出四边形CBA′C′为菱形,根据菱形的性质即可求出A′C的长度,从而得出结论.
解:连接CC′,连接A′C交l于点D,连接AD,此时AD+CD的值最小,如图所示.
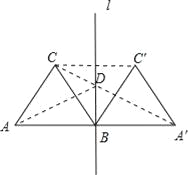

∵△ABC与△A′BC′为正三角形,
∴∠ABC=∠A/=60°,A/B/=BC=A/C/,
∴A/C/∥BC,
∴四边形A/BCC/为菱形,
∴点C关于BC/对称的点是A/,
∴当点D与点B重合时,AD+CD取最小值,
此时AD+CD=2+2=4.
故选A.
“点睛”本题考查了轴对称中的最短线路问题以及等边三角形的性质,找出点C关于BC/对称的点是A/是解题的关键.


科目:初中数学 来源: 题型:
【题目】在学习了正方形后,数学小组的同学对正方形进行了探究,发现:
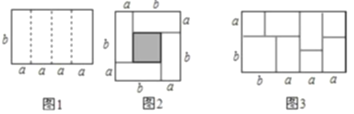
(1)如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB、CD于点M、N . 此时,有结论AE=MN,请进行证明;
(2)如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD, MN 与BD交于点G,连接BF,此时有结论:BF= FG,请利用图2做出证明.
(3)如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N,请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长为![]() 、宽为
、宽为![]() 的长方形,沿中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图).
的长方形,沿中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图).
(1)如图中的阴影部分面积为: ;(用![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)观察如图,请你写出![]() 、
、![]() 、
、![]() 之间的等量关系是 ;
之间的等量关系是 ;
(3)根据(2)中的结论,若![]() ,
,![]() ,则
,则![]() ;
;
(4)实际上通过计算图形的阴影可以探求相应的等式,如图,请你写出这个等式 ;
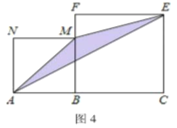
(5)如图,线段![]() (其中
(其中![]() 为正数),点
为正数),点![]() 线在段
线在段![]() 上,在线段
上,在线段![]() 同侧作正方形
同侧作正方形![]() 及正方形
及正方形![]() ,连接
,连接![]() ,
,![]() ,
,![]() 得到
得到![]() .当
.当![]() 时,
时,![]() 的面积记为
的面积记为![]() ;当
;当![]() 时,
时,![]() 的面积记为
的面积记为![]() ;当
;当![]() 时,
时,![]() 的面积记为
的面积记为![]() ;当
;当![]() 时,
时,![]() 的面积记为
的面积记为![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元.
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂购买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于400个,那么为了节约资金.应该选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点A,B,C均在格点上.
(1)请值接写出点A,B,C的坐标.
(2)若平移线段AB,使B移动到C的位置,请在图中画出A移动后的位置D,依次连接B,C,D,A,并求出四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则在①a<0,②b>0,③c<0,④b2﹣4ac>0中错误的个数为( )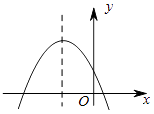
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路灯距地面8米,身高1.6米的小明从距离灯底(点O)20米的点A处,沿AO所在直线行走12米到达点B时,小明身影长度( )
A.变长2.5米
B.变短2米
C.变短2.5米
D.变短3米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过平移,△ABC移到△DEF的位置,如图,下列结论:①AD=BE=CF,且AD∥BE∥CF;②AB∥DE,BC∥EF,BC=EF;③AB=DE,BC=EF,AC=DF.正确的有( )
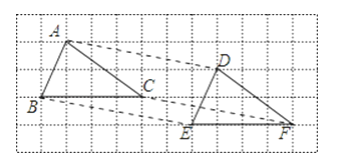
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数 yl= x ( x ≥0 ) , ![]() ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3 ![]() 时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8
④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com