
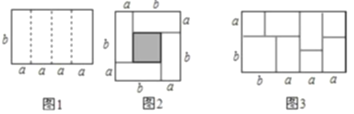
【题目】如图是一个长为![]() 、宽为
、宽为![]() 的长方形,沿中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图).
的长方形,沿中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图).
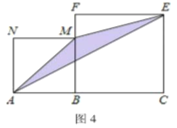
(1)如图中的阴影部分面积为: ;(用![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)观察如图,请你写出![]() 、
、![]() 、
、![]() 之间的等量关系是 ;
之间的等量关系是 ;
(3)根据(2)中的结论,若![]() ,
,![]() ,则
,则![]() ;
;
(4)实际上通过计算图形的阴影可以探求相应的等式,如图,请你写出这个等式 ;
(5)如图,线段![]() (其中
(其中![]() 为正数),点
为正数),点![]() 线在段
线在段![]() 上,在线段
上,在线段![]() 同侧作正方形
同侧作正方形![]() 及正方形
及正方形![]() ,连接
,连接![]() ,
,![]() ,
,![]() 得到
得到![]() .当
.当![]() 时,
时,![]() 的面积记为
的面积记为![]() ;当
;当![]() 时,
时,![]() 的面积记为
的面积记为![]() ;当
;当![]() 时,
时,![]() 的面积记为
的面积记为![]() ;当
;当![]() 时,
时,![]() 的面积记为
的面积记为![]() ,则
,则![]() .
.
【答案】(1) ![]() (2)
(2) ![]() (3) 31;(4)
(3) 31;(4)![]() (5)
(5)![]()
【解析】
(1)阴影部分为边长为(b-a)的正方形,然后根据正方形的面积公式求解;
(2)在图2中,大正方形有小正方形和4个矩形组成,则(a+b)2-(a-b)2=4ab;
(3)由(2)的结论得到(x+y)2-(x-y)2=4xy,再把![]() ,
,![]() 得到
得到![]()
(4)观察图形得到边长为(a+b)与(3a+b)的矩形由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成,则有(a+b)(3a+b)=3a2+4ab+b2.
(5)根据连接BE,则BE∥AM,利用△AME的面积=△AMB的面积即可得出![]()
![]() 即可得出答案.
即可得出答案.
(1)阴影部分为边长为(ba)的正方形,所以阴影部分的面积![]()
故答案为:![]()
(2)图2中,用边长为a+b的正方形的面积减去边长为ba的正方形等于4个长宽分别a、b的矩形面积,
所以![]()
故答案为:![]()
(3)∵![]()
而![]() ,
,![]()
∴![]()
∴![]()
故答案为:31;
(4)边长为(a+b)与(3a+b)的矩形面积为(a+b)(3a+b),它由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成,
∴![]()
故答案为:![]()
(5)连接BE.
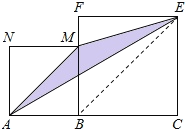
∵在线段AC同侧作正方形ABMN及正方形BCEF,
∴BE∥AM,
∴△AME与△AMB同底等高,
∴△AME的面积=△AMB的面积,
∴当AB=n时,△AME的面积记为![]()
![]()
∴当![]() 时,
时, ![]()
故答案为:![]()


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】科学研究发现,空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系.经测量,在海拔高度为1000米的地方,空气含氧量约为267克/立方米;在海拔高度为2000米的地方,空气含氧量约为235克/立方米.
(1)求出y与x的函数表达式;
(2)求出海拔高度为0米的地方的空气含氧量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新新儿童服装店对“天使”牌服装进行调价,其中A型服装每件的价格上调了10%,B型服装每件的价格下调了5%,已知调价前买这两种服装各一件共花费140元,调价后买3件A型服装和2件B型服装共花费350元,则这两种服装在调价前每件各多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空,并在括号内说明理由:
∵BD平分∠ABC(已知)
∴__________=__________(__________)
又∠1=∠D(已知)
∴__________=__________(__________)
∴__________∥__________(__________)
∴∠ABC+__________=180°(__________)
又∠ABC=55°(已知)
∴∠BCD=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交线段BD于E.
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)画出∠CPQ的角平分线交线段AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
(1)求证:四边形ABEF是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
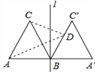
【题目】如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
A. 4 B. 3![]() C. 2
C. 2![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
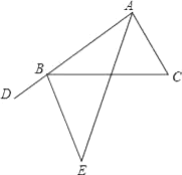
【题目】完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE
(1)求证:∠DBE=∠CBE
证明:∵∠C=∠CBE(已知)
∴BE∥AC________
∴∠DBE=∠DAC________
∵∠DAC=∠C(已知)
∴∠DBE=∠CBE________
(2)请模仿(1)的证明过程,尝试说明∠E=∠BAE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com