练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】科学研究发现，空气含氧量y（克/立方米）与海拔高度x（米）之间近似地满足一次函数关系．经测量，在海拔高度为1000米的地方，空气含氧量约为267克/立方米；在海拔高度为2000米的地方，空气含氧量约为235克/立方米．

    （1）求出y与x的函数表达式；

    （2）求出海拔高度为0米的地方的空气含氧量．

    【答案】（1）；（2）该山山顶处的空气含氧量约为299克/立方米.

    【解析】

    （1）设出一次函数的解析式，利用在海拔高度为1000米的地方，空气含氧量约为267克/立方米；在海拔高度为2000米的地方，空气含氧量约为235克/立方米，代入解析式求出即可；

    （2）根据某山的海拔高度为0米，代入（1）中解析式，求出即可．

    解：（1）设y＝kx+b（k≠0），则有：

    ，

    解得，

    故y＝x+299；

    （2）当x＝0时，y＝299（克/立方米）．

    答：该山山顶处的空气含氧量约为299克/立方米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，以点P为圆心的圆弧与x轴交于A，B两点，已知P（4，2）和A（2，0），则点B的坐标是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

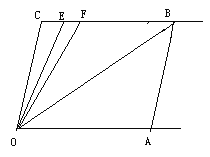
    【题目】如图，直线CB∥OA，∠C=∠A=120°，E、F在CB上，且满足∠FOB=∠AOB，OE平分∠COF．

    （1）求∠EOB的度数；

    （2）若平行移动AB，那么∠OBC：∠OFC的值是否随之发生变化？若变化，找出变化规律或求出变化范围；若不变，求出这个比值；

    （3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=∠OBA？若存在，求出其度数；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

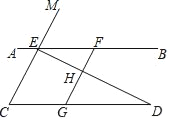
    【题目】如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG交于点H，∠C＝∠EFG，∠CED＝∠GHD．

    （1）求证：CE∥GF；

    （2）试判断∠AED与∠D之间的数量关系，并说明理由；

    （3）若∠EHF＝80°，∠D＝30°，求∠AEM的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人以各自的交通工具、相同路线，前往距离单位10km的培训中心参加学习．图中l甲、l乙分别表示甲、乙前往目的地所走的路程S（km）随时间t（分）变化的函数图象．以下说法：①乙比甲提前12分钟到达；②乙走了8km后遇到甲；③乙出发6分钟后追上甲；④甲走了28分钟时，甲乙相距3km．其中正确的是（　　）

    A. 只有① B. ①③ C. ②③④ D. ①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

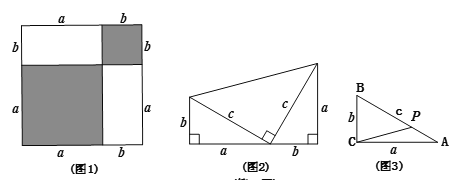
    【题目】（1）用不同的方法计算如图中阴影部分的面积得到的等式： ；

    （2）如图是两个边长分别为、、的直角三角形和一个两条直角边都是的直角三角形拼成，试用不同的方法计算这个图形的面积，你能发现什么？说明理由；

    （3）根据上面两个结论，解决下面问题：若如图中，直角三边a、、c，

    ①满足，ab=18，求的值；

    ②在①的条件下，若点是边上的动点，连接，求线段的最小值；

    ③若，，且，则的值是 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，∠BAD＝60°，AB＝2，E是DC边上一个动点，F是AB边上一点，∠AEF＝30°．设DE＝x，图中某条线段长为y，y与x满足的函数关系的图象大致如图所示，则这条线段可能是图中的（　　）．

    A. 线段EC B. 线段AE C. 线段EF D. 线段BF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在学习了正方形后，数学小组的同学对正方形进行了探究，发现：

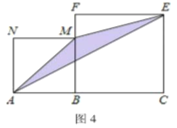
    （1）如图1，在正方形ABCD中，点E为BC边上任意一点（点E不与B、C重合），点F在线段AE上，过点F的直线MN⊥AE，分别交AB、CD于点M、N . 此时，有结论AE=MN，请进行证明；

    （2）如图2：当点F为AE中点时，其他条件不变，连接正方形的对角线BD， MN 与BD交于点G，连接BF，此时有结论：BF= FG，请利用图2做出证明.

    （3）如图3：当点E为直线BC上的动点时，如果（2）中的其他条件不变，直线MN分别交直线AB、CD于点M、N，请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.

    图1 图2 图3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

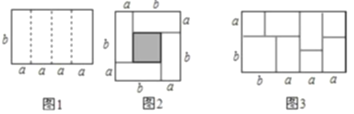
    【题目】如图是一个长为、宽为的长方形，沿中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成的一个“回形”正方形(如图).

    (1)如图中的阴影部分面积为: ；(用、的代数式表示)

    (2)观察如图，请你写出、、之间的等量关系是 ；

    (3)根据(2)中的结论，若，，则 ；

    (4)实际上通过计算图形的阴影可以探求相应的等式，如图，请你写出这个等式 ；

    (5)如图，线段 (其中为正数)，点线在段上，在线段同侧作正方形及正方形，连接，，得到.当时，的面积记为；当时，的面积记为；当时，的面积记为；当时，的面积记为，则 .

    查看答案和解析>>

    同步练习册答案