
【题目】如图,在直角坐标系中,以点P为圆心的圆弧与x轴交于A,B两点,已知P(4,2)和A(2,0),则点B的坐标是 . 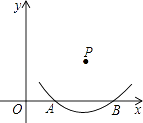
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A.
B.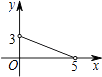
C.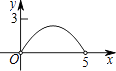
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
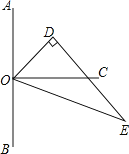
【题目】如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”. 甲同学的解答得到了老师的好评.
乙同学的解答是这样的:“与△ABC相似的三角形只有△AFD,证明如下:
∵DF∥CB,
∴△AFD∽△ABC.”
乙同学的解答正确吗?若不正确,请你改正.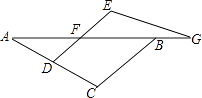
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是 ( ) 
A.新三角形与原三角形相似
B.新矩形与原矩形相似
C.新三角形与原三角形、新矩形与原矩形都相似
D.都不相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级社会实践小组去某商场调查商品的销售情况,了解到该商场以每件80元的价格购进了某品牌衬衫500件,并以每件120元的价格销售了400件,商场准备采取促销措施,将剩下的衬衫降价销售.
(1)每件衬衫降价多少元时,销售完这批衬衫正好达到盈利45%的预期目标?
(2)某公司给员工发福利,在该商场促销钱购买了20件该品牌的衬衫发给员工,后因为有新员工加入,又要购买5件该衬衫,购买这5件衬衫时恰好赶上该商场进行促销活动,求该公司购买这25件衬衫的平均价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若![]() ,求m、n的值.
,求m、n的值.
解:∵![]() ,
,
∴![]()
∴![]() ,而
,而![]() ,
,![]() ,
,
∴![]() 且
且![]() ,
,
∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)![]() ,则a=______;b=_________.
,则a=______;b=_________.
(2)已知△ABC的三边a,b,c满足![]() =0,
=0,
关于此三角形的形状的以下命题:①它是等边三角形;②它属于等腰三角形:③它属于锐角三角形;④它不是直角三角形.其中所有正确命题的序号为________________.
(3)已知△ABC的三边长a、b、c都是正整数,且![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学研究发现,空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系.经测量,在海拔高度为1000米的地方,空气含氧量约为267克/立方米;在海拔高度为2000米的地方,空气含氧量约为235克/立方米.
(1)求出y与x的函数表达式;
(2)求出海拔高度为0米的地方的空气含氧量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com