
【题目】阅读材料:若![]() ,求m、n的值.
,求m、n的值.
解:∵![]() ,
,
∴![]()
∴![]() ,而
,而![]() ,
,![]() ,
,
∴![]() 且
且![]() ,
,
∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)![]() ,则a=______;b=_________.
,则a=______;b=_________.
(2)已知△ABC的三边a,b,c满足![]() =0,
=0,
关于此三角形的形状的以下命题:①它是等边三角形;②它属于等腰三角形:③它属于锐角三角形;④它不是直角三角形.其中所有正确命题的序号为________________.
(3)已知△ABC的三边长a、b、c都是正整数,且![]() ,求△ABC的周长.
,求△ABC的周长.
【答案】(1)2,0;(2)①②③④;(3)7.
【解析】
(1)已知等式利用完全平方公式化简后,再利用非负数的性质求出a与b的值即可;
(2)已知等式变形并利用完全平方公式化简,再利用非负数的性质求出![]() ,进行判断即可.
,进行判断即可.
(3)已知等式变形并利用完全平方公式化简,再利用非负数的性质求出a,b的值,进而确定出三角形周长.
(1)已知等式整理得:![]()
解得:a=2,b=0;
故答案为:2;0;
(2)∵![]()
![]()
![]()
![]()
![]()
①它是等边三角形;②它属于等腰三角形:③它属于锐角三角形;④它不是直角三角形.都正确.
故答案为:①②③④
(3)∵![]()
∴![]()
∴![]()
则a-1=0,b-3=0,解得:a=1,b=3,
由三角形三边关系可知,三角形三边分别为1、3、3,
则△ABC的周长为1+3+3=7.


科目:初中数学 来源: 题型:
【题目】现计划把一批货物用一列火车运往某地![]() 已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元.
已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元.
![]() 设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并求出自变量x的取值范围;
设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并求出自变量x的取值范围;
![]() 已知A型车厢数不少于B型车厢数,运输总费用不低于276000元,问有哪些不同运送方案?
已知A型车厢数不少于B型车厢数,运输总费用不低于276000元,问有哪些不同运送方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′,利用网格点画图和无刻度的直尺画图并解答(保留画图痕迹):
(1)画出△A′B′C′;
(2)画出△ABC的高,即线段BD;
(3)连接AA′、 CC′,那么AA′与CC′的关系是________;线段AC扫过图形的面积为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线 ![]() 交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别为C,D,E,连接OA,OB,0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3 , 则( )
交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别为C,D,E,连接OA,OB,0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3 , 则( )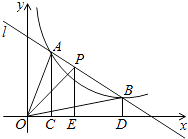
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
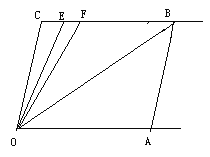
【题目】如图,直线CB∥OA,∠C=∠A=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
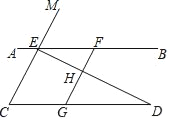
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了正方形后,数学小组的同学对正方形进行了探究,发现:
(1)如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB、CD于点M、N . 此时,有结论AE=MN,请进行证明;
(2)如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD, MN 与BD交于点G,连接BF,此时有结论:BF= FG,请利用图2做出证明.
(3)如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N,请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.

图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com