
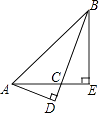
【题目】如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证: ![]() =
= ![]() .
. 
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的三点A、B、C,点A表示的数为5,点B表示的数为-3,点C到点A、点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
(1)点C在数轴上表示的数是______;
(2)当t=______秒时,点P到达点B处:
(3)用含字母t的代数式表示线段AP=______;点P在数轴上表示的数是______.
(4)当P,C之间的距离为1个单位长度时,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A.
B.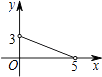
C.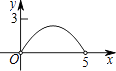
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的边OB上的一点.
(1)过点P画OB的垂线,交OA于点C;
(2)过点P画OA的垂线,垂足为H;
(3)线段PH的长度是点P到______的距离,______是点C到直线OB的距离,线段PC、PH、OC这三条线段大小关系是______(用“<”号连接).
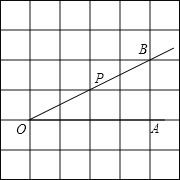
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=APAB;④ABCP=APCB,任选一个,使ΔAPC与ΔACB相似的条件可以是( )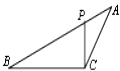
A.①或②或③
B.①或③或④
C.②或③或④
D.①或②或④
查看答案和解析>>
科目:初中数学 来源: 题型:
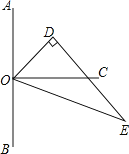
【题目】如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”. 甲同学的解答得到了老师的好评.
乙同学的解答是这样的:“与△ABC相似的三角形只有△AFD,证明如下:
∵DF∥CB,
∴△AFD∽△ABC.”
乙同学的解答正确吗?若不正确,请你改正.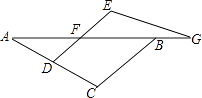
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若![]() ,求m、n的值.
,求m、n的值.
解:∵![]() ,
,
∴![]()
∴![]() ,而
,而![]() ,
,![]() ,
,
∴![]() 且
且![]() ,
,
∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)![]() ,则a=______;b=_________.
,则a=______;b=_________.
(2)已知△ABC的三边a,b,c满足![]() =0,
=0,
关于此三角形的形状的以下命题:①它是等边三角形;②它属于等腰三角形:③它属于锐角三角形;④它不是直角三角形.其中所有正确命题的序号为________________.
(3)已知△ABC的三边长a、b、c都是正整数,且![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com