
【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元.
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂购买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于400个,那么为了节约资金.应该选择哪种方案?
【答案】(1) 甲种机器每台7万元,乙种机器每台5万元;(2)见解析(3)购买甲种机器1台,乙种机器5台.
【解析】
(1)(1)设甲种机器每台x万元,乙种机器每台y万元,根据题意列出二元一次方程组进行求解即可;
(2)设购买甲种机器a台,则购买乙种机器(6﹣a)台,根据题意列出不等式即可进行求解;
(3)算出每种购买方案的求出符合生产要求的机器数,再比较最小资金即可.
解:(1)设甲种机器每台x万元,乙种机器每台y万元.
根据题意得:![]() ,
,
解得:![]() .
.
答:甲种机器每台7万元,乙种机器每台5万元.
(2)设购买甲种机器a台,则购买乙种机器(6﹣a)台.
根据题意:7a+5(6﹣a)≤34,
解得a≤2.
∵a是整数,a≥0,
∴a=0或1或2,
∴有三种购买方案:
①购买甲种机器0台,乙种机器6台;
②购买甲种机器1台,乙种机器5台;
③购买甲种机器2台,乙种机器4台.
(3)方案①所需费用为6×5=30(万元),日产量能力为60×6=360(个),舍去;
方案②所需费用为7+5×5=32(万元),日产量能力为106+60×5=406(个);
方案③所需费用为2×7+4×5=34(万元),日产量能力为106×2+60×4=452(个)
∵32<34,∴选择购买方案②,即购买甲种机器1台,乙种机器5台.


科目:初中数学 来源: 题型:
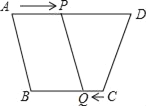
【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=8cm,P,Q分别从A,C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,_____秒后四边形ABQP是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空,并在括号内说明理由:
∵BD平分∠ABC(已知)
∴__________=__________(__________)
又∠1=∠D(已知)
∴__________=__________(__________)
∴__________∥__________(__________)
∴∠ABC+__________=180°(__________)
又∠ABC=55°(已知)
∴∠BCD=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交线段BD于E.
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)画出∠CPQ的角平分线交线段AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
(1)求证:四边形ABEF是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
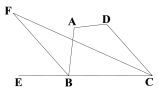
【题目】如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)若BF∥CD,∠ABC=80°,求∠DCB的度数;
(2)已知四边形ABCD中,∠A=105,∠D=125,求∠F的度数;
(3)猜想∠F、∠A、∠D之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
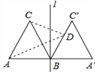
【题目】如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
A. 4 B. 3![]() C. 2
C. 2![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃)t | 20 | 14 | 8 | 2 | ﹣4 | ﹣10 |
根据表中,父亲还给小明出了下面几个问题,请你帮助小明回答下列问题:
(1)表中自变量是 ;因变量是 ;当地面上(即h=0时)时,温度是 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足t与h关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图.
请你根据以上的信息,回答下列问题:
(1)本次共调查了名学生,其中最喜爱戏曲的有人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是 .
(2)根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com