
【题目】实验中学捐资购买了一批物资240吨打算扶贫山区。现有甲、乙、丙三种车型可供选择,每辆车的运载能力和运费如下表所示(每辆车均装满)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨) | 10 | 16 | 20 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元。求甲、乙两种车型各多少辆?
(2)为了节约运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知三种车辆总数为14辆。请求出三种车型分别是多少辆?此时的运费又是多少元?
【答案】(1)需要甲种车型8辆,乙种车型10辆.(2)该市政府调用甲种车型2辆.乙种车型5辆、丙种车型7辆参与运送,此时的运费是7500元.
【解析】
(1)设需要甲种车型x辆,乙种车型y辆,根据抗旱必需物资总240吨且运费为8200元,可得出关于x、y的二元一次方程组,问题可解;
(2)设需要甲种车型m辆,乙种车型n辆,则需要丙种车型(14-m-n)辆,根据抗旱必需物资总240吨,即可得出关于m、n的二元一次方程,结合m、n为正整数即可求出n的值,求出运费后从节约运费入手排除,即可得出结论.
解:(1)设需要甲种车型x辆,乙种车型y辆,
根据题意得:
![]() ,
,
解得:
![]() .
.
答:需要甲种车型8辆,乙种车型10辆.
(2)设需要甲种车型m辆,乙种车型n辆,则需要丙种车型(14-m-n)辆,
根据题意得:10m+16n+20(14-m-n)=240,
∴m=4-![]() n.
n.
∵m、n为正整数,
∴当n=5时,m=2,14-m-n=7,
此时运费为400×2+500×5+600×7=7500(元);
当n=10时,m=0,14-m-n=4,
由题意舍去;∴n=10.
答:该市政府调用甲种车型2辆.乙种车型5辆、丙种车型7辆参与运送,此时的运费是7500元.


科目:初中数学 来源: 题型:
【题目】正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题.
(1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为 ;
(2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点);
(3)人们发现,记格点多边形(顶点均为格点)内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.试确定m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.从纸箱中任意摸出一球,摸到红色球、黄色球的概率分别是0.2、0.3.
(1)试求出纸箱中蓝色球的个数;
(2)小明向纸箱中再放进红色球若干个,小丽为了估计放入的红球的个数,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到红球的频率在0.5附近波动,请据此估计小明放入的红球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
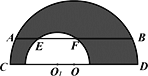
【题目】如图,CD为大半圆的直径,小半圆的圆心O1在线段CD上,大半圆O的弦AB与小半圆O1交于E、F,AB=6cm,EF=2cm,且AB∥CD。则阴影部分的面积为__________cm2(结果保留准确数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③△DEF是轴对称图形;④∠ADE=∠EDO;⑤四边形ABCD面积为EF×BD.其中正确的结论有( )
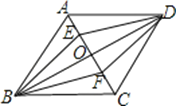
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳某工厂从美国进口A、B两种产品销售,已知每台A种产品进价为3000元,售价为4800元;受中美贸易大战的影响,每台B种产品的进价上涨500元,进口相同数量的B种产品,在中美贸易大战开始之前只需要60万元,中美贸易大战开始之后需要80万元。
(1)中美贸易大战开始之后,每台B种产品的进价为多少?
(2)中美贸易大战开始之后,如果A种产品的进价和售价不变,每台B种产品在进价的基础上提高40%作为售价。公司筹集到不多于35万元且不少于33万元的资金用于进口A、B两种产品共150台,请你设计一种进货方案使销售后的总利润最大。
查看答案和解析>>
科目:初中数学 来源: 题型:
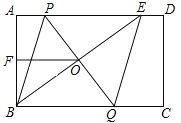
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=4,AD=5,求OE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com