
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=4,AD=5,求OE的长.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】实验中学捐资购买了一批物资240吨打算扶贫山区。现有甲、乙、丙三种车型可供选择,每辆车的运载能力和运费如下表所示(每辆车均装满)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨) | 10 | 16 | 20 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元。求甲、乙两种车型各多少辆?
(2)为了节约运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知三种车辆总数为14辆。请求出三种车型分别是多少辆?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全国两会民生话题成为社会焦点,我市记者为了解百姓“两会民生话题”的聚焦点,随机调查了我市部分市民,并对调查结果进行整理,绘制了如图所示的两幅不完整的统计图表.
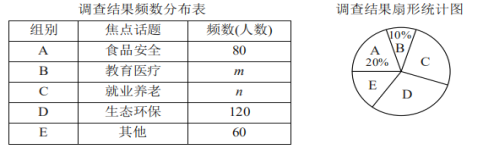
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 %;
(2)我市人口现有650万,请你估计其中关注D组话题的市民人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
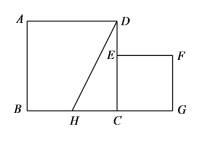
【题目】如图,已知正方形ABCD的边长为1,正方形CEFG的面积为![]() ,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为
,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为![]() ,且
,且![]() .
.
⑴求线段CE的长;
⑵若点H为BC边的中点,连结HD,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD的边BC长上的一点,作DF⊥AE于点F,且满足DF=AB.下面结论:①△DEF≌△DEC;②S△ABE = S△ADF;③AF=AB;④BE=AF.其中正确的结论是( )
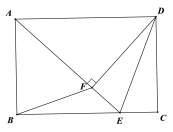
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,CE AB于E, CD平分ECB, 交过点B的射线于D, 交AB于F, 且BC=BD.
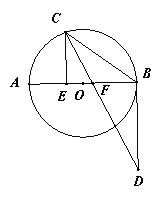
(1)求证:BD是⊙O的切线;
(2)若AE=9, CE=12, 求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 与x轴,y轴分别交于点A,B,将直线AB向右平移6个单位长度,得到直线CD,点A平移后的对应点为点D,点B平移后的对应点为点C.
与x轴,y轴分别交于点A,B,将直线AB向右平移6个单位长度,得到直线CD,点A平移后的对应点为点D,点B平移后的对应点为点C.
(1)求点C的坐标;
(2)求直线CD的表达式;
(3)若点B关于原点的对称点为点E,设过点E的直线![]() ,与四边形ABCD有公共点,结合函数图象,求k的取值范围.
,与四边形ABCD有公共点,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
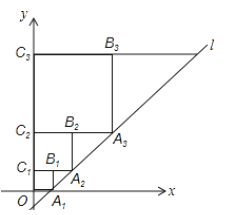
【题目】在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则点B2019的横坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学着说点理:补全证明过程:
如图,已知![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .请补充证明过程,并在括号内填上相应的理由.
.请补充证明过程,并在括号内填上相应的理由.
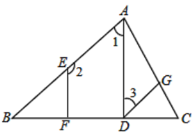
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (___________________),
(___________________),
∴![]() (___________________),
(___________________),
∴________![]() (___________________).
(___________________).
又∵![]() (已知),
(已知),
∴![]() (___________________),
(___________________),
∴![]() ________(___________________),
________(___________________),
∴![]() (___________________).
(___________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com