
【题目】学着说点理:补全证明过程:
如图,已知![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .请补充证明过程,并在括号内填上相应的理由.
.请补充证明过程,并在括号内填上相应的理由.
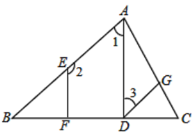
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (___________________),
(___________________),
∴![]() (___________________),
(___________________),
∴________![]() (___________________).
(___________________).
又∵![]() (已知),
(已知),
∴![]() (___________________),
(___________________),
∴![]() ________(___________________),
________(___________________),
∴![]() (___________________).
(___________________).
【答案】垂直的定义;同位角相等,两直线平行;∠1;两直线平行,同旁内角互补;同角的补角相等;DG;内错角相等,两直线平行;两直线平行,同位角相等.
【解析】
根据平行线的判定和性质,垂直的定义,同角的补角相等知识一一判断即可.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°(垂直的定义),
∴EF∥AD(同位角相等,两直线平行),
∴∠1+∠2=180°(两直线平行,同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3(同角的补角相等),
∴AB∥DG(内错角相等,两直线平行),
∴∠GDC=∠B(两直线平行,同位角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠1;两直线平行,同旁内角互补;同角的补角相等;DG;内错角相等,两直线平行;两直线平行,同位角相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=4,AD=5,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:已知Rt△ABC的周长为30,斜边长c=13,求△ABC的面积.、
解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c=①______,
因为c=13,所以a+b=②______,
所以(a+b)2=③______,所以a2+ b2+④_____=289.
因为a2+b2=c2,所以c2+2ab=289,
所以⑤______+2ab=289,所以ab=⑥______(第1步),
所以△ABC的面积=![]() ab=
ab=![]() ×⑦______=⑧______(第2步).
×⑦______=⑧______(第2步).
合作探究:(1)对解法展示进行填空.
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是______(填序号).
①整体思想;②数形结合思想;③分类讨论思想.
方法迁移:
(3)已知一直角三角形的面积为24,斜边长为10,求这个直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
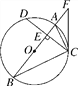
【题目】如图,在⊙O中,直径AB⊥弦CD于点E,连接AC,BC,点F是BA延长线上的一点,且∠FCA=∠B.
(1)求证:CF是⊙O的切线;
(2)若AE=4,tan∠ACD=![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
科目:初中数学 来源: 题型:
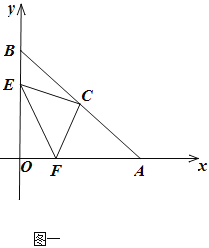
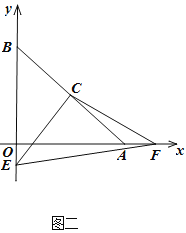
【题目】如图,RtΔOAB中,点O(0,0),点A(6,0),点B(0,6),斜边AB的中点C.
点E从点B出发,沿BO方向,点F从点O出发,沿OA方向,速度都是1个单位/秒,时间是t秒,连接CE、CF、EF,
(1)直接写出C点坐标______.
(2)判断ΔCEF的形状,并证明;
(3)在0<t<6时,以C、E、F、O四点组成的四边形面积是否发生变化?不变,求出这个值;变化,用含t的式子表示;
(4)在t>6时,以C、E、F、O四点组成的四边形面积是否发生变化?不变,求出这个值;变化,用含t的式子表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
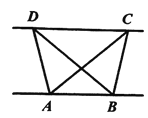
【题目】(1)探究新知:如图1,已知![]() 与
与![]() 的面积相等,试判断
的面积相等,试判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
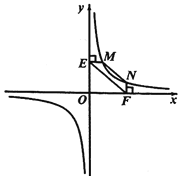
(2)结论应用:
①如图2,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图像上,过点
的图像上,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,连接
,连接![]() .试证明:
.试证明:![]() .
.
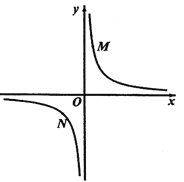
②若①中的其他条件不变,只改变点![]() ,
,![]() 的位置如图3所示,请画出图形,判断
的位置如图3所示,请画出图形,判断![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com