
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

【答案】(1)证明见解析(2)![]()
【解析】分析:(1)由矩形ABCD中,O为BD的中点,易证得△PDO≌△QBO(ASA),继而证得OP=OQ;(2)AD=8cm,AP=tcm,即可用t表示PD的长;
(3)由四边形PBQD是菱形,可得PB=PD,即可得AB+AP=PD,继而可得方程6+t=(8-t),解此方程即可求得答案
本题解析:.
解:(1)∵四边形ABCD是矩形,∴AD∥BC,
∴∠PDO=∠QBO,∵O为BD的中点,∴DO=BO,
在△PDO和△QBO中,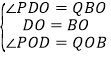
∴△PDO≌△QBO(ASA),∴OP=OQ;
(2)由题意知:AD=8cm,AP=tcm,∴PD=8﹣t,
(3)∵PB=PD,∴PB2=PD2,即AB2+AP2=PD2,
∴62+t2=(8-t)2,解得 t=![]() ,
,
∴当t=![]() 时,PB=PD.
时,PB=PD.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
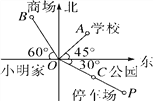
【题目】如图是小明家和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的是哪些地方?
(2)学校、商场和停车场分别在小明家的什么方位?
(3)如果学校距离小明家400m,那么商场和停车场分别距离小明家多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块三角板的直角顶点重合.
(1)写出以点C为顶点的相等的角;
(2)若∠ACB=150°,求∠DCE的度数;
(3)写出∠ACB与∠DCE之间所具有的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示.设点A,B,C所对应数的和是p.

(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是一幅“苹果排列图”,第一行有1个苹果,第二行有2个,第三行有4个,第四行有8个,….你是否发现苹果的排列规律?猜猜看,第十行有_____个苹果;第n行有_____ 个苹果.(可用乘方形式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
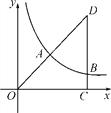
【题目】如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
(1)求该反比例函数的表达式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是生活中常见的月历表,你对它了解吗?
(1)如果下表是另一个月的月历表,a表示该月中某一天,b,c,d是该月中其他3天,那么b,c,d与a有什么关系?b=________;c=________;d=________(用含a的式子填空).

(2)用一个长方形框圈出月历表中的三个数(如上表中的阴影),若这三个数之和等于51,则这三个数各是多少?
(3)这样圈出的三个数之和可能是64吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com