
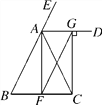
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

【答案】已知:①③(或①④或②④或③④),证明见解析.
【解析】试题分析:根据平行四边形的判定方法就可以组合出不同的结论,然后即可证明.
其中解法一是证明两组对角相等的四边形是平行四边形;
解法二是证明两组对边平行的四边形是平行四边形;
解法三是证明一组对边平行且相等的四边形是平行四边形;
解法四是证明两组对角相等的四边形是平行四边形.
试题解析:已知:①③,①④,②④,③④均可,其余均不可以.
解法一:
已知:在四边形ABCD中,①AD∥BC,③∠A=∠C,
求证:四边形ABCD是平行四边形.
证明:∵AD∥BC,
∴∠A+∠B=180°,∠C+∠D=180°.
∵∠A=∠C,
∴∠B=∠D.
∴四边形ABCD是平行四边形.
解法二:
已知:在四边形ABCD中,①AD∥BC,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
又∵AD∥BC,
∴四边形ABCD是平行四边形;
解法三:
已知:在四边形ABCD中,②AB=CD,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形;
解法四:
已知:在四边形ABCD中,③∠A=∠C,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
∴∠A+∠D=180°,
又∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形.


科目:初中数学 来源: 题型:
【题目】操作探究:
数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条ABCD,其中AD=BC=1,AB=CD=5.然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:

探究:
(1)若∠1=70°,∠MKN= °;
(2)改变折痕MN位置,△MNK始终是 三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积最小值为![]() ,此时∠1的大小可以为 °
,此时∠1的大小可以为 °
(4)小明继续动手操作,发现了△MNK面积的最大值.请你求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
(1)求证:AC=FG;
(2)当AC⊥FG时,△ABC应是怎样的三角形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是一个多面体的展开图,每个面上都标注了字母(字母均在外表面),请根据要求回答下列问题:
(1)如果面A在多面体的上面,那么哪一面在底部?
(2)如果面F在前面,从右面看是面B,那么哪一面在上面?
(3)如果从左面看是面C,面D在后面,那么哪一面在上面?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4 cm,AD=12 cm,点P在AD边上以每秒1 cm的速度从点A向点D运动,点Q在BC边上,以每秒4 cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,当运动时间=_____时线段PQ∥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD的平分线与∠ADC的平分线相交于点E,∠ABC的平分线与∠BCD的平分线相交于点F,则∠E与∠F的数量关系是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车沿公路左右行驶,向左为正,向右为负,某天从A地出发后到收工回家所走的路线如下:![]() 单位:千米
单位:千米![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 问收工时离出发点A多少千米?
问收工时离出发点A多少千米?
![]() 若该出租车每千米耗油
若该出租车每千米耗油![]() 升,问从A地出发到收工共耗油多少升?
升,问从A地出发到收工共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们所学的课本中,多项式与多项式相乘可以用几何图形的面积来表示.例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式:____________.

【答案】(a+2b)(2a+b)=2a2+5ab+2b2
【解析】试题分析:图②的面积可以用长为a+a+b,宽为b+a+b的长方形面积求出,也可以由四个正方形与5个小长方形的面积之和求出,表示出即可.
解:根据图形列得:(a+2b)(2a+b)=2a2+5ab+2b2.
故答案为:(a+2b)(2a+b)=2a2+5ab+2b2.
考点:多项式乘多项式.
点评:此题考查了多项式乘以多项式法则,熟练掌握法则是解本题的关键.
【题型】填空题
【结束】
18
【题目】若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如3=22-12,16=52-32,则3和16是智慧数).已知按从小到大的顺序构成如下数列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,…则第2 013个“智慧数”是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com