
����Ŀ������̽����
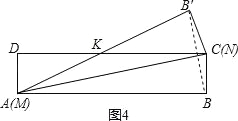
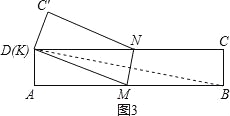
��ѧ�о����ϣ���ʦ������̽������ֽ�е���ѧ���⡷ʱ����ʾ��ͼ1��ʾ�ij�����ֽ��ABCD������AD=BC=1��AB=CD=5��Ȼ����ֽ�������⻭һ�����߶�MN����ֽƬ��MN�۵���MB��DN���ڵ�K���õ���MNK����ͼ2��ʾ��

̽����
��1������1=70������MKN= ����
��2���ı��ۺ�MNλ�ã���MNKʼ���� �����Σ���˵�����ɣ�
Ӧ�ã�
��3�������Խ��С�����о���MNK�����ʱ������KN���ϵĸ�ʼ���Ǹ������ֵ��������һ���֣����ܿ��о�����KMN�������СֵΪ![]() ����ʱ��1�Ĵ�С����Ϊ ��
����ʱ��1�Ĵ�С����Ϊ ��
��4��С���������ֲ�������������MNK��������ֵ���������������ֵ��

���𰸡�(1)��40��(2)��������(3)��45����135��(4)�����ֵΪ1.3��
��������
�����������1�������ݾ��ε����ʺ��۵������������KNM����KMN�Ķ����������������ڽǺͼ�����⣻
(2)�����÷��۱任�������Լ���ֱ��ƽ���ڴ�����ȵó�KM=KN��(3)�����õ���KMN�������СֵΪ![]() ʱ��KN=BC=1����KN��B��M���ó���1=��NMB=45����ͬ������ֽ�������۵�ʱ����1=��NMB=135����(4)�������һ��������ֽƬ���ۣ�ʹ��B��D�غϣ���ʱ��KҲ��D�غϣ��������������ֽƬ�ضԽ���AC���ۣ���ʱ�ۺۼ�ΪAC�������������⣮
ʱ��KN=BC=1����KN��B��M���ó���1=��NMB=45����ͬ������ֽ�������۵�ʱ����1=��NMB=135����(4)�������һ��������ֽƬ���ۣ�ʹ��B��D�غϣ���ʱ��KҲ��D�غϣ��������������ֽƬ�ضԽ���AC���ۣ���ʱ�ۺۼ�ΪAC�������������⣮
�����������1������ͼ1�� ���ı���ABCD�Ǿ��Σ� ��AM��DN�� ���KNM=��1�� �ߡ�1=70����
���KNM=��KMN=��1=70���� ���MKN=40����
(2)�������� ���ɣ���AB��CD�����1=��MND�� ����ֽƬ��MN�۵��� BGFYTTTQ ���1=��KMN����MND=��KMN��
��KM=KN��
(3)����ͼ2������KMN�������СֵΪ![]() ʱ��KN=BC=1����KN��B��M�� �ߡ�NMB=��KMN����KMB=90����
ʱ��KN=BC=1����KN��B��M�� �ߡ�NMB=��KMN����KMB=90����
���1=��NMB=45����ͬ������ֽ�������۵�ʱ����1=��NMB=135����
(4)�������������
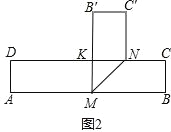
���һ����ͼ3��������ֽƬ���ۣ�ʹ��B��D�غϣ���ʱ��KҲ��D�غϣ� MK=MB=x����AM=5��x��
�ɹ��ɶ�����12+��5��x��2=x2�� ���x=2.6�� ��MD=ND=2.6�� S��MNK=S��MND=![]() ��1��2.6=1.3��
��1��2.6=1.3��
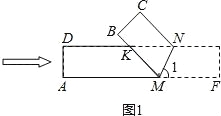
���������ͼ4��������ֽƬ�ضԽ���AC���ۣ���ʱ�ۺۼ�ΪAC�� MK=AK=CK=x����DK=5��x��
ͬ���ɵ�MK=NK=2.6�� ��MD=1�� ��S��MNK=![]() ��1��2.6=1.3�� ��MNK��������ֵΪ1.3��
��1��2.6=1.3�� ��MNK��������ֵΪ1.3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB�ߵĴ�ֱƽ����l1��BC�ڵ�D��AC�ߵĴ�ֱƽ����l2��BC�ڵ�E��l1��l2�ཻ�ڵ�O������0B��OC������ADE���ܳ�Ϊ6cm����OBC���ܳ�Ϊ16cm��
��1�����߶�BC�ij���
��2������OA�����߶�OA�ij���
��3������BAC=120�㣬���DAE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʳƷ��ȫ���ϰ��չ�ע�Ļ��⣬��ʳƷ�����ӹ��������Ӽ��������к��������������Ӽ�����������������ʳƷ�Ĵ�������䣮ij���ϼӹ���������A��B�������Ͼ������ͬ�����Ӽ���A����ÿƿ��Ӹ����Ӽ�2�ˣ�B����ÿƿ��Ӹ����Ӽ�3�ˣ���֪270�˸����Ӽ�ǡ��������A��B�������Ϲ�100ƿ����A��B�������ϸ������˶���ƿ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
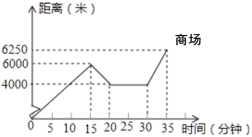
����Ŀ��С����ĩ��絥���Ӽҳ���ȥ�̳���������������һ��·ʱ������Ҫ��һ���飬����ԭ·���ص��վ������»���꣬���������ǰ���̳�����ͼ������ҵľ�����ʱ��Ĺ�ϵ ʾ��ͼ�������ͼ���ṩ����Ϣ�ش��������⣺
��1��С���Ӽҵ��»�����·���Ƕ����ף�
��2��С�����»����ͣ���˶��ٷ��ӣ�
��3������꣬С�����»���굽�̳��������ٶ��Ƕ�����/���ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=2x�ͷ�����������ͼ���ڵ�A��m����2����
��1�����������Ľ���ʽ��
��2���۲�ͼ��ֱ��д������������ֵ���ڷ���������ֵʱ�Ա���x��ȡֵ��Χ��
��3����˫�����ϵ�C��2��n����OA����ƽ�� ![]() ����λ���ȵõ���B���ж��ı���OABC����״��֤����Ľ��ۣ�
����λ���ȵõ���B���ж��ı���OABC����״��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
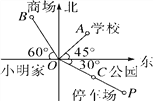
����Ŀ����ͼ��С���Һ�ѧУ���ڵصļ�ͼ����֪OA��2cm��OB��2.5cm��OP��4cm����CΪOP���е㣬�ش��������⣺
(1)ͼ�о�С���Ҿ�����ͬ������Щ�ط���
(2)ѧУ���̳���ͣ�����ֱ���С���ҵ�ʲô��λ��
(3)���ѧУ����С����400m����ô�̳���ͣ�����ֱ����С���Ҷ�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=ax+b��a��0�������κ���y=ax2+bx�ͷ���������y= ![]() ��k��0����ͬһֱ������ϵ�е�ͼ����ͼ��ʾ��A�������Ϊ����2��0���������н����У���ȷ���ǣ� ��
��k��0����ͬһֱ������ϵ�е�ͼ����ͼ��ʾ��A�������Ϊ����2��0���������н����У���ȷ���ǣ� �� 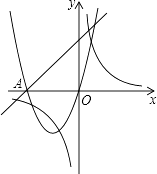
A.b=2a+k
B.a=b+k
C.a��b��0
D.a��k��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ�����ͼ����A��2��1����B����1����3����
��1�����һ�κ����Ľ���ʽ��
��2�����һ�κ�����ͼ����x�ᡢy��Ľ������ꣻ
��3�����һ�κ�����ͼ��������������Χ�ɵ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ĸ���ϵ�У�ѡ������ǡ���Ĺ�ϵ��Ϊ�������Ƴ��ı���ABCD��ƽ���ı��Σ�������֤������д��һ�ּ��ɣ�
��ϵ����AD��BC����AB=CD���ۡ�A=��C���ܡ�B+��C=180�㣮
��֪�����ı���ABCD�У�����������������������������
��֤���ı���ABCD��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com