
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 ![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
【答案】
(1)
解:设反比例函数的解析式为y= ![]() (k>0),
(k>0),
∵A(m,﹣2)在y=2x上,
∴﹣2=2m,
∴m=﹣1,
∴A(﹣1,﹣2),
又∵点A在y= ![]() 上,
上,
∴k=2,
∴反比例函数的解析式为y= ![]()
(2)
解:观察图象可知正比例函数值大于反比例函数值时自变量x的取值范围为﹣1<x<0或x>1
(3)
解:四边形OABC是菱形.
证明:∵A(﹣1,﹣2),
∴OA= ![]() =
= ![]() ,
,
由题意知:CB∥OA且CB= ![]() ,
,
∴CB=OA,
∴四边形OABC是平行四边形,
∵C(2,n)在y= ![]() 上,
上,
∴n=1,
∴C(2,1),
OC= ![]() =
= ![]() ,
,
∴OC=OA,
∴四边形OABC是菱形
【解析】(1)设反比例函数的解析式为y= ![]() (k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式;(2)直接由图象得出正比例函数值大于反比例函数值时自变量x的取值范围;(3)首先求出OA的长度,结合题意CB∥OA且CB=
(k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式;(2)直接由图象得出正比例函数值大于反比例函数值时自变量x的取值范围;(3)首先求出OA的长度,结合题意CB∥OA且CB= ![]() ,判断出四边形OABC是平行四边形,再证明OA=OC即可判定出四边形OABC的形状.
,判断出四边形OABC是平行四边形,再证明OA=OC即可判定出四边形OABC的形状.


科目:初中数学 来源: 题型:
【题目】如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF.
(1)试说明:△ABC≌△DFE;
(2)若BF=13,EC=7,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.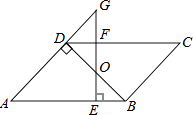
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[![]() ]=1.现对72进行如下操作:72
]=1.现对72进行如下操作:72![]() [
[![]() ]=8
]=8![]() [
[![]() ]=2
]=2![]() [
[![]() ]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________.
]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:
数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条ABCD,其中AD=BC=1,AB=CD=5.然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:

探究:
(1)若∠1=70°,∠MKN= °;
(2)改变折痕MN位置,△MNK始终是 三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积最小值为![]() ,此时∠1的大小可以为 °
,此时∠1的大小可以为 °
(4)小明继续动手操作,发现了△MNK面积的最大值.请你求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为4的正方形,在正方形的一个角上剪去长方形CEFG,其中E,G分别是边CD,BC上的点,且CE=3,CG=2,剩余部分是六边形ABGFED,请你建立适当的直角坐标系求六边形ABGFED各顶点的坐标.
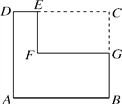
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( ) 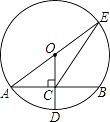
A.2 ![]()
B.8
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4 cm,AD=12 cm,点P在AD边上以每秒1 cm的速度从点A向点D运动,点Q在BC边上,以每秒4 cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,当运动时间=_____时线段PQ∥AB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com