
【题目】如图,将两块三角板的直角顶点重合.
(1)写出以点C为顶点的相等的角;
(2)若∠ACB=150°,求∠DCE的度数;
(3)写出∠ACB与∠DCE之间所具有的数量关系.

【答案】(1)见解析;(2) 30°;(3) ∠ACB+∠DCE=180°.
【解析】(1)根据同角的余角相等作答即可;
(2)由图得∠DCE=90°﹣∠ACE,求∠ACE的度数即可;
(3)∠ACB+∠DCE=∠BCE+∠ACE+∠DCE=90°+90°=180°.
(1)根据同角的余角相等可得:∠ACE=∠BCD,ACD=∠ECB;
(2)∵∠ACB=150°,∠BCE=90°,∴∠ACE=150°﹣90°=60°,
∴∠DCE=90°﹣∠ACE=90°﹣60°=30°,
(3)∵∠ACB+∠DCE=∠BCE+∠ACE+∠DCE=90°+90°=180°,
∴∠ACB+∠DCE=180°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)

查看答案和解析>>
科目:初中数学 来源: 题型:
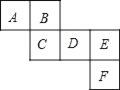
【题目】如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B,C相对的面分别是 ;
(2)若A=a3+![]() a2b+3,B=﹣
a2b+3,B=﹣![]() a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣![]() (a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=![]() ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.
(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
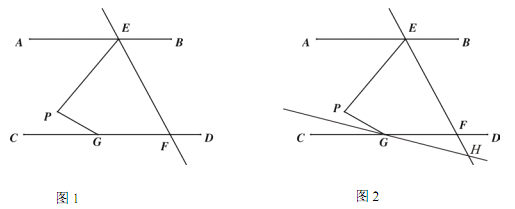
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是一个多面体的展开图,每个面上都标注了字母(字母均在外表面),请根据要求回答下列问题:
(1)如果面A在多面体的上面,那么哪一面在底部?
(2)如果面F在前面,从右面看是面B,那么哪一面在上面?
(3)如果从左面看是面C,面D在后面,那么哪一面在上面?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题 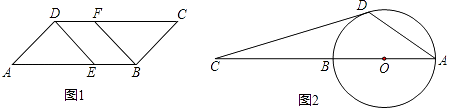
(1)如图1,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF;
(2)如图2,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,沿AC方向开山修建一条公路,为了加快施工进度,要在小山的另一边寻找点E同时施工,从AC上的一点B取∠ABD=150°,沿BD的方向前进,取∠BDE=60°,测得BD=520m,BC=80m,并且AC,BD和DE在同一平面内,那么公路CE段的长度为( ) 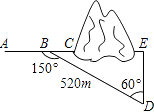
A.180m
B.260 ![]() m
m
C.(260 ![]() ﹣80)m
﹣80)m
D.(260 ![]() ﹣80)m
﹣80)m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com