
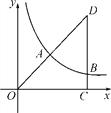
【题目】如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
(1)求该反比例函数的表达式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的表达式.
【答案】(1)![]() ;(2)y=-
;(2)y=-![]() x+3.
x+3.
【解析】分析:(1)根据线段的中点坐标的求法(线段中点的横纵坐标分别是线段2个端点的横纵坐标的和的一半)易得点A坐标,设出反比例函数的解析式,把A坐标代入即可;
(2)点B,D的横坐标相等,代入(1)中反比例函数的解析式中,求出点B的坐标,把A、B的坐标代入一次函数解析式,利用待定系数法求出函数解析式即可.
本题解析: (1)由题意,易得点A的坐标是(1.5,2),则该反比例函数的表达式为y=![]() .
.
(2)把x=3代入y=![]() ,得y=1,则点B的坐标是(3,1).
,得y=1,则点B的坐标是(3,1).
设过A、B两点的直线的表达式为y=kx+b,
则![]() 解得
解得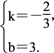
则过A、B两点的直线的表达式为y=-![]() x+3.
x+3.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
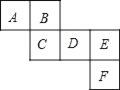
【题目】如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B,C相对的面分别是 ;
(2)若A=a3+![]() a2b+3,B=﹣
a2b+3,B=﹣![]() a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣![]() (a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题 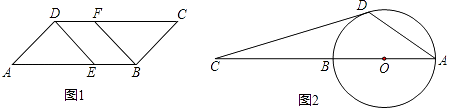
(1)如图1,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF;
(2)如图2,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车沿公路左右行驶,向左为正,向右为负,某天从A地出发后到收工回家所走的路线如下:![]() 单位:千米
单位:千米![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 问收工时离出发点A多少千米?
问收工时离出发点A多少千米?
![]() 若该出租车每千米耗油
若该出租车每千米耗油![]() 升,问从A地出发到收工共耗油多少升?
升,问从A地出发到收工共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE , 其中结论正确的个数为( )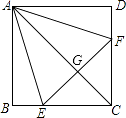
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,沿AC方向开山修建一条公路,为了加快施工进度,要在小山的另一边寻找点E同时施工,从AC上的一点B取∠ABD=150°,沿BD的方向前进,取∠BDE=60°,测得BD=520m,BC=80m,并且AC,BD和DE在同一平面内,那么公路CE段的长度为( ) 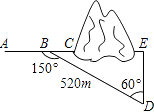
A.180m
B.260 ![]() m
m
C.(260 ![]() ﹣80)m
﹣80)m
D.(260 ![]() ﹣80)m
﹣80)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图B,E,C,F, 四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断 △ABC≌△DEF 的是 ( )
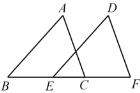
A. ∠A=∠D B. DF∥AC C. AC=DF D. AB=DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com