
【题目】如图B,E,C,F, 四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断 △ABC≌△DEF 的是 ( )
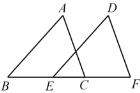
A. ∠A=∠D B. DF∥AC C. AC=DF D. AB=DE
【答案】C
【解析】由EB=CF可得出BC=EF,A、由∠A=∠D、∠ABC=∠DEF、BC=EF,利用全等三角形的判定定理AAS即可证出△ABC≌△DEF;B、由DF∥AC可得出∠ACB=∠DFE,结合BC=EF、∠ABC=∠DEF,利用全等三角形的判定定理ASA即可证出△ABC≌△DEF;C、由AC=DF结合∠ABC=∠DEF、BC=EF,无法证出△ABC≌△DEF;D、由AB=DE结合∠ABC=∠DEF、BC=EF,利用全等三角形的判定定理SAS即可证出△ABC≌△DEF.综上即可得出结论.
∵EB=CF,
∴BC=EF.
A、在△ABC和△DEF中,
 ,
,
∴△ABC≌△DEF(AAS);
B、∵DF∥AC,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
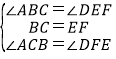 ,
,
∴△ABC≌△DEF(ASA);
C、在△ABC和△DEF中,
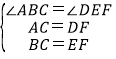 ,
,
无法证出△ABC≌△DEF;
D、在△ABC和△DEF中,
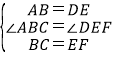 ,
,
∴△ABC≌△DEF(SAS).
故选:C.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
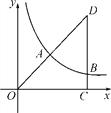
【题目】如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
(1)求该反比例函数的表达式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是生活中常见的月历表,你对它了解吗?
(1)如果下表是另一个月的月历表,a表示该月中某一天,b,c,d是该月中其他3天,那么b,c,d与a有什么关系?b=________;c=________;d=________(用含a的式子填空).

(2)用一个长方形框圈出月历表中的三个数(如上表中的阴影),若这三个数之和等于51,则这三个数各是多少?
(3)这样圈出的三个数之和可能是64吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是棱长为a的小正方体,如图②、如图③是由若干这样相同的小正方体摆放而成,按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层中小正方体的个数为s(提示:第一层中,s=1;第二层中,s=3),则第n层中,s=________.(用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点 A 表示的有理数为﹣4,点 B 表示的有理数为 6,点 P 从 点 A 出发以每秒 2 个单位长度的速度在数轴上沿由 A 到 B 方向运动,当点 P 到 达点 B 后立即返回,仍然以每秒 2 个单位长度的速度运动至点 A 停止运动.设 运动时间为 t(单位:秒).
(1)求 t=2 时点 P 表示的有理数;
(2)求点 P 是 AB 的中点时 t 的值;
(3)在点 P 由点 A 到点 B 的运动过程中,求点 P 与点 A 的距离(用含 t 的代数式表示);
(4)在点 P 由点 B 到点 A 的返回过程中,点 P 表示的有理数是多少(用含 t 的 代数式表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一项工程,在工程招标时,接到甲、乙两个工程队的投标书,施工一天,需付甲工程队工程款1.5万元,乙工程队工程款1.1万元,工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用5天;
(3)若甲、乙两队合作4天,余下的工程由乙队单独也正好如期完成.
在不耽误工期的情况下,你觉得那一种施工方案最节省工程款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)普通列车的行驶路程为________千米;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2 ![]() ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将
,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 ![]() 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为
绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 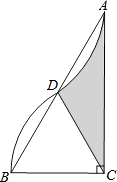
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买A、B两种品牌的显示器共120台,A、B两种品牌显示器的单价分别为800元和1000元,设购买A品牌显示器x台,若学校购买这两种品牌显示器的总费用为110000元,那么A、B两种品牌的显示器各购买了多少台?根据题目信息完成上面的表格,并列出方程,列出的方程: .
项目品牌 | 单价/元 | 购买数量/台 | 购买费用/元 |
A | 800 | x |
|
B | 1000 |
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com