
【题目】(1)探究新知:如图1,已知![]() 与
与![]() 的面积相等,试判断
的面积相等,试判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)结论应用:
①如图2,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图像上,过点
的图像上,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,连接
,连接![]() .试证明:
.试证明:![]() .
.
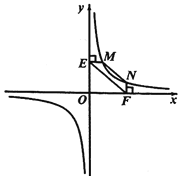
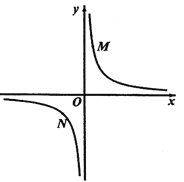
②若①中的其他条件不变,只改变点![]() ,
,![]() 的位置如图3所示,请画出图形,判断
的位置如图3所示,请画出图形,判断![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
【答案】(1)![]() ,理由见解析;(2)①见解析;②
,理由见解析;(2)①见解析;②![]() ,理由见解析.
,理由见解析.
【解析】
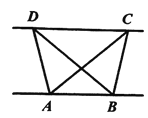
(1)分别过点C,D,作CG⊥AB,DH⊥AB,垂足为G,H,则∠CGA=∠DHB=90°,根据△ABC与△ABD的面积相等,证明AB与CD的位置关系;
(2)连结MF,NE,设点M的坐标为(x1,y1),点N的坐标为(x2,y2),进一步证明S△EFM=S△EFN,结合(1)的结论即可得到MN∥EF;
(3)连接FM、EN、MN,结合(2)的结论证明出MN∥EF,GH∥MN,于是证明出EF∥GH.
(1)如图1,分别过点![]() 、
、![]() 作
作![]() 、
、![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,
,

则![]() ,
,
∴![]() ,
,
∵![]() 且
且![]() ,
,
![]() ,
,
∴![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ;
;
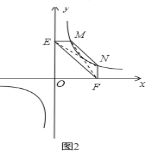
(2)①如图2,连接![]() ,
,![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() ,
,![]() 在反比例函数的图像上,
在反比例函数的图像上,
∴![]() ,
,![]() .
.
∵![]() 轴,
轴,![]() 轴,且点
轴,且点![]() ,
,![]() 在第一象限,
在第一象限,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,
从而,由(1)中的结论可知:![]() ;
;
②如图
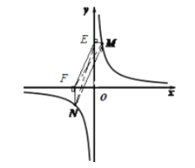
![]() ,
,
理由:连接![]() ,
,![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
由(2)①同理可得:
![]() ,
,![]() ,
,
∴![]() ,
,
从而,由(1)中的结论可知:![]() .
.


科目:初中数学 来源: 题型:
【题目】学着说点理:补全证明过程:
如图,已知![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .请补充证明过程,并在括号内填上相应的理由.
.请补充证明过程,并在括号内填上相应的理由.
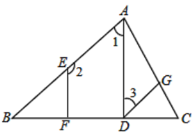
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (___________________),
(___________________),
∴![]() (___________________),
(___________________),
∴________![]() (___________________).
(___________________).
又∵![]() (已知),
(已知),
∴![]() (___________________),
(___________________),
∴![]() ________(___________________),
________(___________________),
∴![]() (___________________).
(___________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年新年时,小明的爸爸收到这样一条短信,年龄与数字的秘密!如果你年龄在1~99之间,那么你随便想一个数字,就能算出你的年龄!计算步骤如下:
①随便想一个1~9之间的数字.
②把这个数字乘以 5.
③然后加上 40.
④再乘以 20.
⑤把所得的数加上 1219.
⑥用最后得到的数减去你出生的年份,这样你会得到一个数,它的第一个数字就是你开始想的那个数,后面的数字就表示你的实际年龄(实际年龄=当前年份-出生年份).
小明马上想了一个数字“8”,他是2007年出生的,请你帮他计算一下,验证这条短信所说的是否正确.假设小明当时想的数字为![]() ,请用所学的代数式知识列式解开这条短信的奥秘.
,请用所学的代数式知识列式解开这条短信的奥秘.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,点
中,点![]() 是直线
是直线![]() 上一点.连接
上一点.连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() .
.
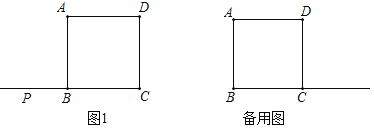
(1)如图1.若点![]() 在线段
在线段![]() 的延长线上过点
的延长线上过点![]() 作
作![]() 于
于![]() .与对角线
.与对角线![]() 交于点
交于点![]() .
.
①请仔细阅读题目,根据题意在图上补全图形;②求证:![]() .
.
(2)若点![]() 在射线
在射线![]() 上,直接写出
上,直接写出![]() ,
,![]() ,
,![]() 三条线段之间的数量关系(不必写过程).
三条线段之间的数量关系(不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要利用一面墙(墙长为25米)建一个矩形场地,用100米的围栏围成三个大小相同的矩形,设矩形的边长AB为x米,矩形场地的总面积为y平方米.
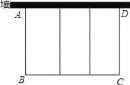
(1)请用含有x的式子表示y(不要求写出x的取值范围);
(2)当x为何值时,矩形场地的总面积为400平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有![]() 、
、![]() 、
、![]() 、
、![]() 四个点表示的数分别为:-3、-1、2、4,如下图.
四个点表示的数分别为:-3、-1、2、4,如下图.
![]()
(1)计算![]() 、
、![]() 、
、![]() ;再观察数轴,写出
;再观察数轴,写出![]() 、
、![]() 的距离,
的距离,![]() 、
、![]() 两点的距离,和
两点的距离,和![]() 、
、![]() 两点的距离.
两点的距离.
(2)请用![]() 、
、![]() 或
或![]() 填空:
填空:![]() 、
、![]() 的距离______
的距离______![]() ,
,![]() 、
、![]() 两点的距离______
两点的距离______![]() ,
,![]() 、
、![]() 两点的距离______
两点的距离______![]() .
.
(3)如果点![]() 、
、![]() 两点表示的数分别为
两点表示的数分别为![]() ,
,![]() ,那么
,那么![]() 、
、![]() 两点的距离=______.
两点的距离=______.
(4)若![]() ,数
,数![]() 代表的点
代表的点![]() 在数轴上什么位置?
在数轴上什么位置?![]() 介于哪两个数之间?
介于哪两个数之间?
查看答案和解析>>
科目:初中数学 来源: 题型:
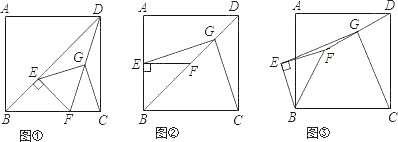
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)请问EG与CG存在怎样的数量关系,并证明你的结论;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com