
【题目】在正方形![]() 中,点
中,点![]() 是直线
是直线![]() 上一点.连接
上一点.连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() .
.
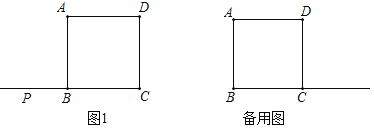
(1)如图1.若点![]() 在线段
在线段![]() 的延长线上过点
的延长线上过点![]() 作
作![]() 于
于![]() .与对角线
.与对角线![]() 交于点
交于点![]() .
.
①请仔细阅读题目,根据题意在图上补全图形;②求证:![]() .
.
(2)若点![]() 在射线
在射线![]() 上,直接写出
上,直接写出![]() ,
,![]() ,
,![]() 三条线段之间的数量关系(不必写过程).
三条线段之间的数量关系(不必写过程).
【答案】(1)①见解析;②见解析;(2)EC=![]() (CD-PC)或EC=
(CD-PC)或EC=![]() (CD+PC)
(CD+PC)
【解析】
(1)①构建题意画出图形即可;②想办法证明△APB≌△PEH即可;
(2)结论:当点P在线段BC上时:![]() .当点P在线段BC的延长线上时:
.当点P在线段BC的延长线上时:![]() ,构造全等三角形即可解决问题.
,构造全等三角形即可解决问题.
解:(1)①补全图形如图所示.
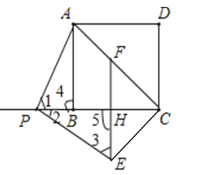
②证明:![]() 线段
线段![]() 绕点
绕点![]() 顺时针能转
顺时针能转![]() 得到线段
得到线段![]() ,
,
![]()
![]() ,
,![]()
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,
![]()
![]()
![]() 于
于![]() ,
,
![]()
![]()
![]()
![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
![]() .
.
![]()
![]() ,
,
![]()
![]() ,
,
∴![]() ;
;
(2)当点P在线段BC上时:![]() .
.
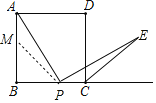
理由:在BA上截取BM=BP.则△PBM是等腰直角三角形,PM=![]() PB.
PB.
易证△PCE≌△AMP,可得EC=PM,
∵CD-PC=BC-PC=PB,
∴EC=PM=![]() PB=
PB=![]() (CD-PC),
(CD-PC),
当点P在线段BC的延长线上时:![]() .
.
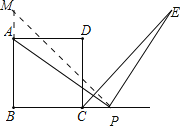
理由:在BA上截取BM=BP.则△PBM是等腰直角三角形,PM=![]() PB.
PB.
易证△PCE≌△AMP,可得EC=PM,
∵CD+PC=BC+PC=PB,
∴EC=PM=![]() PB=
PB=![]() (CD+PC).
(CD+PC).
故答案为EC=![]() (CD-PC)或EC=
(CD-PC)或EC=![]() (CD+PC).
(CD+PC).


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
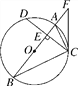
【题目】如图,在⊙O中,直径AB⊥弦CD于点E,连接AC,BC,点F是BA延长线上的一点,且∠FCA=∠B.
(1)求证:CF是⊙O的切线;
(2)若AE=4,tan∠ACD=![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角板的直角顶点放在点O处.(注:∠DOE=90°)
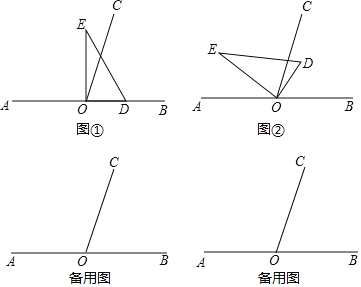
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O转动,如果OD在∠BOC的内部,且∠BOD=50°,求∠COE的度数;
(3)将直角三角板DOE绕点O转动,如果OD在∠BOC的外部,且∠BOD=80°,请在备用图中画出三角板DOE的位置,并求出∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)如图,Rt△ABC中,C= 90o,以斜边AB为边向外作正方形 ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6![]() ,则另一直角边BC的长为 ▲ .
,则另一直角边BC的长为 ▲ .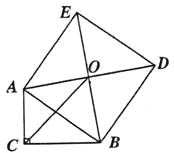
查看答案和解析>>
科目:初中数学 来源: 题型:
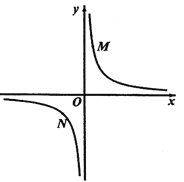
【题目】(1)探究新知:如图1,已知![]() 与
与![]() 的面积相等,试判断
的面积相等,试判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)结论应用:
①如图2,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图像上,过点
的图像上,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,连接
,连接![]() .试证明:
.试证明:![]() .
.
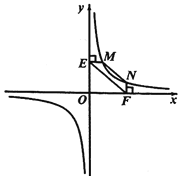
②若①中的其他条件不变,只改变点![]() ,
,![]() 的位置如图3所示,请画出图形,判断
的位置如图3所示,请画出图形,判断![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
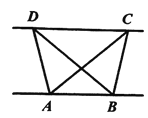
【题目】如图,要在平行四边形![]() 内作一个菱形.甲,乙两位同学的作法分别如下:
内作一个菱形.甲,乙两位同学的作法分别如下:

对于甲乙两人的作法,可判断( )
A.甲正确,乙错误B.甲错误,乙正确C.甲,乙均正确D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮将笔记本电脑水平放置在桌子上,显示屏OA与底板OB所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架BCO'后,电脑转到B O′A′位置(如图3),侧面示意图为图4.已知OA=OB=28cm,O′C⊥OB于点C,O′C=14cm.
(参考数据:![]() ,
,![]() ,
,![]() )
)
(1)求∠CBO'的度数.
(2)显示屏的顶部A'比原来升高了多少cm?(结果精确到0.1cm)
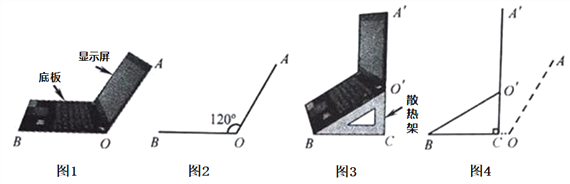
(3)如图4,垫入散热架后,要使显示屏O′A′与水平线的夹角仍保持120°,则显示屏O′A′应绕点O'按顺时针方向旋转多少度?(不写过程,只写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华周一早展起来,步行到离家900米的学校去上学,到了学校他发现数学课本忘在家中了,于是他立即按照原路步行回家,拿到数学课本后立即按照原路改骑自行车返回学校,已知小华骑自行车的速度是他步行速度的3倍,步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟. 小华骑自行车的速度是多少米每分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com