
����Ŀ����ͼ����ֱ��AB��һ��OΪ�˵�������OC��ʹ��BOC=70������һ��ֱ�����ǰ��ֱ�Ƕ�����ڵ�O������ע����DOE=90����
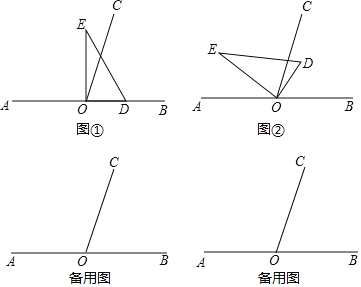
��1����ͼ������ֱ�����ǰ�DOE��һ��OD��������OB�ϣ�����COE=�� ������
��2����ͼ������ֱ�����ǰ�DOE�Ƶ�Oת�������OD����BOC���ڲ�������BOD=50��������COE�Ķ�����
��3����ֱ�����ǰ�DOE�Ƶ�Oת�������OD����BOC���ⲿ������BOD=80�������ڱ���ͼ�л������ǰ�DOE��λ�ã��������COE�Ķ�����
���𰸡���1��20������2����COE�Ķ���Ϊ70������3����ͼ����������COE�Ķ���Ϊ100����60����
��������
��1����ͼ�٣���ֱ�����ǰ�DOE��һ��OD��������OB�ϣ����COE=20�㣻
��2����ͼ�ڣ���ֱ�����ǰ�DOE�Ƶ�Oת�������OD�ڡ�BOC���ڲ����ҡ�BOD=50�㣬��֪��COD=20���������COE�Ķ�����
��3����ֱ�����ǰ�DOE�Ƶ�Oת�������OD�ڡ�BOC���ⲿ���ҡ�BOD=80�㣬�ڱ���ͼ�л������ǰ�DOE������λ�ã����������COE�Ķ�����
��1����ͼ�٣���ֱ�����ǰ�DOE��һ��OD��������OB�ϣ����COE=��DOE����BOC=90�㩁70��=20�㣮
�ʴ�Ϊ��20�㣻
��2����ͼ�ڣ���ֱ�����ǰ�DOE�Ƶ�Oת�������OD�ڡ�BOC���ڲ���
�ߡ�BOD=50�㣬
���COD=��BOC����BOD=70�㩁50��=20�㣬
���COE=��DOE����COD=90�㩁20��=70�㣬
�𣺡�COE�Ķ���Ϊ70�㣻
��3����ֱ�����ǰ�DOE�Ƶ�Oת�������OD�ڡ�BOC���ⲿ���ҡ�BOD=80�㣬������������ۣ�
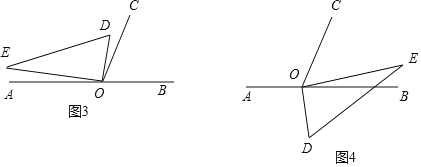
��ͼ3�У��ߡ�BOD=80�㣬��BOC=70�㣬
���DOC=��BOD����BOC=10�㣬
���COE=��COD+��DOE=10��+90��=100�㣮
��ͼ4�У��ߡ�BOE=��DOE����BOD=90�㩁80��=10�㣬
���COE=��BOC����BOE=70�㩁10��=60�㣮
������������COE�Ķ���Ϊ100���60�㣮
�𣺡�COE�Ķ���Ϊ100���60�㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˽�ס�����������Ա������������������Ӽס����������Ÿ������ȡ20��Ա���������������ܲ��ԣ����Գɼ����ٷ��ƣ����£�
��7886 748175768770759075798170748086698377
��9373 888172819483778380817081737882807040
��˵�����ɼ�80�ּ�����Ϊ���㣬70-79��Ϊ���ã�60-69��Ϊ�ϸ�60������Ϊ���ϸ�
��1��������������
���� | ƽ���� | ��λ�� | ���� |
�� | 78.3 | 75 | |
�� | 78 | 80.5 |
��2�����������ݿ����ƶϳ� ����Ա������������ˮƽ�ϸߣ���˵�����ɣ������ٴ�������ͬ�ĽǶ�˵���ƶϵĺ����ԣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽�����۲����е�ʽ��
��1����ʽ��![]()
��2����ʽ��![]()
��3����ʽ��![]()
��4����ʽ��![]()
��ش��������⣺
��1�������Ϲ���д����5����ʽ��= ___________ = ___________
��2���ú�n��ʽ�ӱ�ʾ��n����ʽ��= ___________ = ___________(nΪ��������
��3����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BPƽ�֡�ABC��DΪBP��һ�㣬E��F�ֱ���BA��BC�ϣ�������DE��DF������BED��140�������BFD�Ķ����ǣ�������

A. 40��B. 50��C. 60��D. 70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵���2014����2016���ڼ�����һ����У�2014�꣬���̵���3500Ԫ������������в���ȫ�����ꣻ2016�꣬������еĽ��۱�2014���½���11Ԫ/�У����̵���2400Ԫ��������2014����ͬ���������Ҳȫ�����꣬��е��ۼ۾�Ϊ60Ԫ/�У�
��1��2014��������еĽ����Ƕ���Ԫ/�У�
��2�������̵�ÿ��������������������������������ͬ�������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��̽������Щ����Ľǿ�����һ�����ǰ廭����
�ڢ�![]() ����
����![]() ����
����![]() ����
����![]() �У�С��ͬѧ����һ�����ǰ廭���������������_________��������ţ�
�У�С��ͬѧ����һ�����ǰ廭���������������_________��������ţ�
��2����̽�������У������Խ��С��������ͼ�ε��˶���ʽ�ж���.��ͼ�����������ǰ廭����ֱ��![]() ��Ȼ��һ�����ǰ�ƴ����һ������
��Ȼ��һ�����ǰ�ƴ����һ������![]() �ǣ�
�ǣ�![]() ���Ķ�����
���Ķ�����![]() �ǣ�
�ǣ�![]() ���Ķ��㻥���غϣ��ұ�
���Ķ��㻥���غϣ��ұ�![]() ��
��![]() ����ֱ��
����ֱ��![]() ��.�̶����ǰ�
��.�̶����ǰ�![]() �����������ǰ�
�����������ǰ�![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����תһ���Ƕ�
��˳ʱ�뷽����תһ���Ƕ�![]() ������
������![]() ������
������![]() ��һ���غ�ʱֹͣ.
��һ���غ�ʱֹͣ.

�ٵ�![]() ƽ��
ƽ��![]() ʱ������ת�Ƕ�
ʱ������ת�Ƕ�![]() ��
��
���������![]() �������ڣ�����ת�Ƕ�
�������ڣ�����ת�Ƕ�![]() ���������ڣ���˵������.
���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019������ʱ��С���İְ��յ�����һ�����ţ����������ֵ����ܣ������������1~99֮�䣬��ô�������һ�����֣��������������䣡���㲽�����£�
�������һ��1~9֮������֣�
�ڰ�������ֳ��� 5��
��Ȼ����� 40��
���ٳ��� 20��
�ݰ����õ������� 1219��
�������õ�������ȥ���������ݣ��������õ�һ���������ĵ�һ�����־����㿪ʼ����Ǹ�������������־ͱ�ʾ���ʵ�����䣨ʵ������=��ǰ���-������ݣ���
С����������һ�����֡�8��������2007������ģ������������һ�£���֤����������˵���Ƿ���ȷ������С����ʱ�������Ϊ![]() ��������ѧ�Ĵ���ʽ֪ʶ��ʽ��������ŵİ��أ�
��������ѧ�Ĵ���ʽ֪ʶ��ʽ��������ŵİ��أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �У���
�У���![]() ��ֱ��
��ֱ��![]() ��һ��.����
��һ��.����![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ���õ��߶�
���õ��߶�![]() ������
������![]() .
.
��1����ͼ1.����![]() ���߶�
���߶�![]() ���ӳ����Ϲ���
���ӳ����Ϲ���![]() ��
��![]() ��
��![]() .��Խ���
.��Խ���![]() ���ڵ�
���ڵ�![]() .
.
������ϸ�Ķ���Ŀ������������ͼ�ϲ�ȫͼ�Σ�����֤��![]() .
.
��2������![]() ������
������![]() �ϣ�ֱ��д��
�ϣ�ֱ��д��![]() ��
��![]() ��
��![]() �����߶�֮���������ϵ������д���̣�.
�����߶�֮���������ϵ������д���̣�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
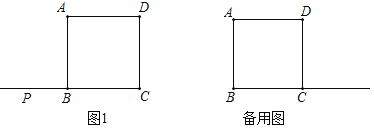
����Ŀ����ͼ,��Rt��ABC��,��ACB=90��,����C��ֱ��MN��AB,DΪAB����һ��,����D��DE��BC,��ֱ��MN�ڵ�E,����ΪF,����CD,BE
��1����֤:CE=AD
��2����DΪAB���е�,���A�Ķ�������ʲô����ʱ,�ı���BECD�������Σ���˵������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com