
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE
(1)求证:CE=AD
(2)若D为AB的中点,则∠A的度数满足什么条件时,四边形BECD是正方形?请说明理由.

【答案】(1)见解析;(2) 当∠A=45°时,四边形BECD是正方形,理由见解析.
【解析】分析:(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;
(2)求出四边形BECD是平行四边形,根据直角三角形的斜边上的中线求出 CD=BD,根据菱形的判定,和正方形的判定推出即可.
详解:(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
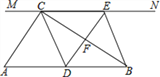
(2)解:当∠A=45°时,四边形BECD是正方形,
理由如下:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,AD=BD
∴∠CDB=90°,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
∴四边形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】2016年9月28日-12月31日,山东临沂灯展中千万盏彩灯点亮300亩天然花海.某日,从晚上17时开始每小时进入灯展的人数约为900人(之前该灯展有游客400人),同时每小时走出灯展的人数约为600人,已知该灯展的饱和人数约为1600人,则该灯展人数饱和时的时间约为( )
A. 21时 B. 22时 C. 23时 D. 24时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
(1)把圆片沿数轴向右滚动半周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.
①第 次滚动后,A点距离原点最近,第 次滚动后,A点距离原点最远.
②当圆片结束运动时,A点运动的路程共有 ,此时点A所表示的数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC. 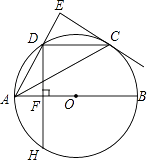
(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)![]()
(3)![]()
(4)[ 2![]() - (
- (![]() )×24 ]÷5×(- 1)2001
)×24 ]÷5×(- 1)2001
(5)![]()
(6) -22 -(-1)2001×(![]() -
- ![]() )÷
)÷![]() +(-3)2
+(-3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某班学生上学的三种方式(乘车、步行、骑车)的人数分布直方图和扇形图2. 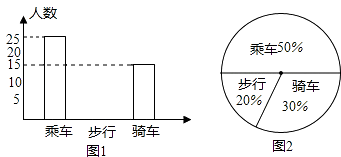
(1)该班有多少名学生;
(2)补上人数分布直方图的空缺部分;
(3)若全年级有800人,估计该年级步行有名学生.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P1(x1 , y1),P2(x2 , y2)在反比例函数y= ![]() (k>0)的图像上,且x1=﹣x2 , 则( )
(k>0)的图像上,且x1=﹣x2 , 则( )
A.y1<y2
B.y1=y2
C.y1>y2
D.y1=﹣y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,AD与OC交于点E,连接CD、OD,给出以下四个结论: ①AC∥OD;②CE=OE;③∠CDE=∠COD;④2CD2=CEAB.
其中正确结论的序号是(在横线上填上你认为所有正确结论的代号).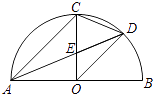
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴被折成90°,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2018将与圆周上的数字________重合.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com