
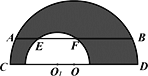
【题目】如图,CD为大半圆的直径,小半圆的圆心O1在线段CD上,大半圆O的弦AB与小半圆O1交于E、F,AB=6cm,EF=2cm,且AB∥CD。则阴影部分的面积为__________cm2(结果保留准确数)
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A所表示的数是![]() ,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
(1)在数轴上描出点B;
(2)求点C所表示的数,并在数轴上描出点C;
(3)已知在数轴上存在点P,使PA+PC=PB,求点P所表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,相距![]() 千米的
千米的![]() 两地间有一条笔直的马路,
两地间有一条笔直的马路,![]() 地位于
地位于![]() 两地之间且距
两地之间且距![]() 地
地![]() 千米,小明同学骑自行车从
千米,小明同学骑自行车从![]() 地出发沿马路以每小时
地出发沿马路以每小时![]() 千米的速度向
千米的速度向![]() 地匀速运动,当到达
地匀速运动,当到达![]() 地后立即以原来的速度返回,到达
地后立即以原来的速度返回,到达![]() 地停止运动,设运动时间为(时),小明的位置为点
地停止运动,设运动时间为(时),小明的位置为点![]() .
.
![]()
(1)当![]() 时,求点
时,求点![]() 间的距离
间的距离
(2)当小明距离![]() 地
地![]() 千米时,直接写出所有满足条件的
千米时,直接写出所有满足条件的![]() 值
值
(3)在整个运动过程中,求点![]() 与点
与点![]() 的距离(用含的代数式表示)
的距离(用含的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某一城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天;若由甲队先做20天,剩下的工程由甲、乙两队合做完成.
(1)甲、乙两队合作多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数![]() 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )
的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学捐资购买了一批物资240吨打算扶贫山区。现有甲、乙、丙三种车型可供选择,每辆车的运载能力和运费如下表所示(每辆车均装满)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨) | 10 | 16 | 20 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元。求甲、乙两种车型各多少辆?
(2)为了节约运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知三种车辆总数为14辆。请求出三种车型分别是多少辆?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
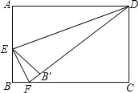
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
A. 2![]() ﹣2B. 6C. 2
﹣2B. 6C. 2![]() ﹣2D. 4
﹣2D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】惠民新村分给小慧家一套价格为12万元的住房.按要求,需首期(第一年)付房款3万元,从第二年起,每年应付房款0.5万元与上一年剩余房款的利息的和.假设剩余房款年利率为0.4%,小慧列表推算如下:
第一年 | 第二年 | 第三年 | … | |
应还款(万元) | 3 |
|
| … |
剩余房款(万元) | 9 | 8.5 | 8 | … |
若第![]() 年小慧家仍需还款,则第
年小慧家仍需还款,则第![]() 年应还款_______万元(
年应还款_______万元(![]() >1).
>1).
查看答案和解析>>
科目:初中数学 来源: 题型:
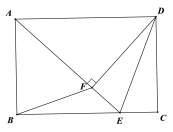
【题目】如图,点E为矩形ABCD的边BC长上的一点,作DF⊥AE于点F,且满足DF=AB.下面结论:①△DEF≌△DEC;②S△ABE = S△ADF;③AF=AB;④BE=AF.其中正确的结论是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com