
ЁОЬтФПЁПЮЊЩюЛЏвхЮёНЬг§ПЮГЬИФИяЃЌТњзубЇЩњЕФИіадЛЏбЇЯАашЧѓЃЌФГаЃОЭЁАбЇЩњЖджЊЪЖЭиеЙЃЌЬхг§ЬиГЄЁЂвеЪѕЬиГЄКЭЪЕМљЛюЖЏЫФРрбЁПЮвтЯђЁБНјааСЫГщбљЕїВщЃЈУПШЫбЁБЈвЛРрЃЉЃЌЛцжЦСЫШчЭМЫљЪОЕФСНЗљЭГМЦЭМЃЈВЛЭъећЃЉЃЌЧыИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓЩШаЮЭГМЦЭМжаmЕФжЕЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉдкБЛЕїВщЕФбЇЩњжаЃЌЫцЛњГщвЛШЫЃЌГщЕНбЁЁАЬхг§ЬиГЄРрЁБЛђЁАвеЪѕЬиГЄРрЁБЕФбЇЩњЕФИХТЪЪЧЖрЩйЃП

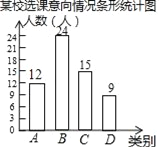
ЃЈ3ЃЉвбжЊИУаЃга800УћбЇЩњЃЌМЦЛЎПЊЩшЁАЪЕМљЛюЖЏРрЁБПЮГЬУПАрАВХХ20ШЫЃЌЮЪбЇаЃПЊЩшЖрЩйИіЁАЪЕМљЛюЖЏРрЁБПЮГЬЕФАрМЖБШНЯКЯРэЃП
ЁОД№АИЁПЃЈ1ЃЉ20ЃЈ2ЃЉ![]() ЃЈ3ЃЉПЊЩш10ИіЁАЪЕбщЛюЖЏРрЁБПЮГЬЕФАрМЖЪ§БШНЯКЯРэ
ЃЈ3ЃЉПЊЩш10ИіЁАЪЕбщЛюЖЏРрЁБПЮГЬЕФАрМЖЪ§БШНЯКЯРэ
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнCРрШЫЪ§га15ШЫЃЌеМзмШЫЪ§ЕФ25%ПЩЕУГізмШЫЪ§ЃЌЧѓГіAРрШЫЪ§ЃЌНјЖјПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉжБНгИљОнИХТЪЙЋЪНПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЧѓГіЁАЪЕМљЛюЖЏРрЁБЕФзмШЫЪ§ЃЌНјЖјПЩЕУГіНсТлЃЎ
ЯъНтЃКЃЈ1ЃЉзмШЫЪ§=15ЁТ25%=60ЃЈШЫЃЉЃЎAРрШЫЪ§=60Љ24Љ15Љ9=12ЃЈШЫЃЉЃЎ
Ёп12ЁТ60=0.2=20%ЃЌЁрm=20ЃЎ
ЬѕаЮЭГМЦЭМШчЭМЃЛ
ЃЈ2ЃЉГщЕНбЁЁАЬхг§ЬиГЄРрЁБЛђЁАвеЪѕЬиГЄРрЁБЕФбЇЩњЕФИХТЪ=![]() =
=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁп800ЁС25%=200ЃЌ200ЁТ20=10ЃЌ
ЁрПЊЩш10ИіЁАЪЕбщЛюЖЏРрЁБПЮГЬЕФАрМЖЪ§БШНЯКЯРэЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЗжзщКЯзїбЇЯАЁБвбГЩЮЊЭЦЖЏПЮЬУНЬбЇИФИяЃЌДђдьзджїИпаЇПЮЬУЕФживЊДыЪЉ.ФГжабЇДгШЋаЃбЇЩњжаЫцЛњГщШЁВПЗжбЇЩњЖдЁАЗжзщКЯзїбЇЯАЁБЪЕЪЉКѓЕФбЇЯАаЫШЄЧщПіНјааЕїВщЗжЮіЃЌЭГМЦЭМШчЯТЃК

ЧыНсКЯЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓГіЫцЛњГщШЁЕїВщЕФбЇЩњШЫЪ§ЃЛ
ЃЈ2ЃЉВЙШЋЗжзщКѓбЇЩњбЇЯАаЫШЄЕФЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉЗжзщКѓбЇЩњбЇЯАаЫШЄЮЊЁАжаЁБЕФЫљеМЕФАйЗжБШКЭЖдгІЩШаЮЕФдВаФНЧ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
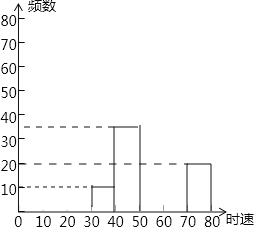
ЁОЬтФПЁПЫцзХГЕСОЕФдіМгЃЌНЛЭЈЮЅЙцЕФЯжЯѓдНРДдНбЯжиЃЌНЛОЏЖдШЫУёТЗФГРзДяВтЫйЧјМьВтЕНЕФвЛзщЦћГЕЕФЪБЫйЪ§ОнНјааећРэЃЈЫйЖШдк30Љ40КЌЦ№ЕужЕ30ЃЌВЛКЌжеЕужЕ40ЃЉЃЌЕУЕНЦфЦЕЪ§МАЦЕТЪШчБэЃК
Ъ§ОнЖЮ | ЦЕЪ§ | ЦЕТЪ |
30Љ40 | 10 | 0.05 |
40Љ50 | 36 | c |
50Љ60 | a | 0.39 |
60Љ70 | b | d |
70Љ80 | 20 | 0.10 |
змМЦ | 200 | 1 |
ЃЈ1ЃЉБэжаaЁЂbЁЂcЁЂdЗжБ№ЮЊЃКaЃНЁЁ ЁЁЃЛ bЃНЁЁ ЁЁЃЛ cЃНЁЁ ЁЁЃЛ dЃНЁЁ ЁЁ
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉШчЙћЦћГЕЪБЫйВЛЕЭгк60ЧЇУзМДЮЊЮЅеТЃЌдђЮЅеТГЕСОЙВгаЖрЩйСОЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋКЏЪ§![]() ЕФЭМЯѓбиyжсЯђЩЯЦНвЦЕУЕНвЛЬѕаТКЏЪ§ЕФЭМЯѓЃЌЦфжаЕуAЃЈ-4ЃЌmЃЉЃЌBЃЈ-1ЃЌnЃЉ,ЦНвЦКѓЕФЖдгІЕуЗжБ№ЮЊЕуA'ЁЂB'.ШєЧњЯпЖЮABЩЈЙ§ЕФУцЛ§ЮЊ9ЃЈЭМжаЕФвѕгАВПЗжЃЉЃЌдђаТЭМЯѓЕФКЏЪ§БэДяЪНЪЧ ЃЈ ЃЉ
ЕФЭМЯѓбиyжсЯђЩЯЦНвЦЕУЕНвЛЬѕаТКЏЪ§ЕФЭМЯѓЃЌЦфжаЕуAЃЈ-4ЃЌmЃЉЃЌBЃЈ-1ЃЌnЃЉ,ЦНвЦКѓЕФЖдгІЕуЗжБ№ЮЊЕуA'ЁЂB'.ШєЧњЯпЖЮABЩЈЙ§ЕФУцЛ§ЮЊ9ЃЈЭМжаЕФвѕгАВПЗжЃЉЃЌдђаТЭМЯѓЕФКЏЪ§БэДяЪНЪЧ ЃЈ ЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌA, BЪЧжБЯпlЩЯЕФСНЕуЃЌЕуBЙигкADЕФЖдГЦЕуЮЊMЃЌСЌНг![]() НЛADгкFЕу.
НЛADгкFЕу.
ЃЈ1ЃЉШє![]() ЃЌШчЭМЃЌ
ЃЌШчЭМЃЌ
ЂйвРЬтвтВЙШЋЭМаЮЃЛ
ЂкХаЖЯMFгыFCЕФЪ§СПЙиЯЕЪЧ ЃЛ

ЃЈ2ЃЉШчЭМЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌCDЕФбгГЄЯпЯрНЛгкЕуEЃЌШЁ
ЃЌCDЕФбгГЄЯпЯрНЛгкЕуEЃЌШЁ![]() EЕФжаЕуHЃЌСЌНсHF. гУЕШЪНБэЪОЯпЖЮCEгыAFЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
EЕФжаЕуHЃЌСЌНсHF. гУЕШЪНБэЪОЯпЖЮCEгыAFЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН4ЃЌADЃН6ЃЌEЪЧABБпЕФжаЕуЃЌFЪЧЯпЖЮBCЩЯЕФЖЏЕуЃЌНЋЁїEBFбиEFЫљдкжБЯпелЕўЕУЕНЁїEBЁфFЃЌСЌНгBЁфDЃЌдђBЁфDЕФзюаЁжЕЪЧЃЈЁЁЁЁЃЉ
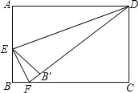
A. 2![]() Љ2B. 6C. 2
Љ2B. 6C. 2![]() Љ2D. 4
Љ2D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
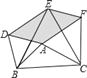
ЁОЬтФПЁПШчЭМЃЌвдЁїABCЕФШ§БпЮЊБпдкBCЕФЭЌвЛВрЗжБ№зїШ§ИіЕШБпШ§НЧаЮЃЌМДЁїABDЁЂЁїBCEЁЂЁїACFЃЌЧыЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЫФБпаЮADEFЪЧЪВУДЫФБпаЮЃП
ЃЈ2ЃЉЕБЁїABCТњзуЪВУДЬѕМўЪБЃЌЫФБпаЮADEFЪЧОиаЮЃП
ЃЈ3ЃЉЕБЁїABCТњзуЪВУДЬѕМўЪБЃЌвдAЁЂDЁЂEЁЂFЮЊЖЅЕуЕФЫФБпаЮВЛДцдкЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
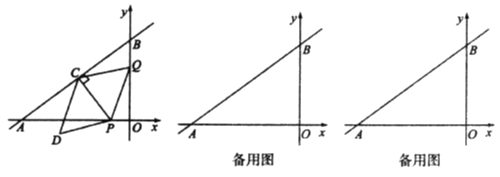
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() гы
гы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№НЛгкЕу
жсЗжБ№НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() жсИКЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЭЌЪБЖЏЕу
жсИКЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЭЌЪБЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌбиЩфЯп
ГіЗЂЃЌбиЩфЯп![]() ЗНЯђвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЙ§Еу
ЗНЯђвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌвд
ЃЌвд![]() ЁЂ
ЁЂ![]() ЮЊСкБпЙЙдьЦНааЫФБпаЮ
ЮЊСкБпЙЙдьЦНааЫФБпаЮ![]() ЃЌЩшЕу
ЃЌЩшЕу![]() дЫЖЏЕФЪБМфЮЊ
дЫЖЏЕФЪБМфЮЊ![]() s.
s.
ЃЈ1ЃЉЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌгУКЌ
ЩЯЪБЃЌгУКЌ![]() ЕФДњЪ§ЪНБэЪО
ЕФДњЪ§ЪНБэЪО![]() ЁЂ
ЁЂ![]() ЕФГЄ.
ЕФГЄ.
ЃЈ2ЃЉдкдЫЖЏЙ§ГЬжаЃЌЂйЕБЕу![]() Тфдк
Тфдк![]() жсЩЯЪБЃЌЧѓГіТњзуЬѕМўЕФ
жсЩЯЪБЃЌЧѓГіТњзуЬѕМўЕФ![]() ЕФжЕ;ЂкЕБЕу
ЕФжЕ;ЂкЕБЕу![]() Тфдк
Тфдк![]() ФкВП(ВЛАќРЈБпНч)ЪБЃЌжБНгаДГі
ФкВП(ВЛАќРЈБпНч)ЪБЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ЃЈ3ЃЉзїЕу![]() Йигк
Йигк![]() жсЕФЖдГЦЕу
жсЕФЖдГЦЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГЪБПЬЪЙЙ§
ЃЌдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГЪБПЬЪЙЙ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЕФдВгы
Ш§ЕуЕФдВгы![]() Ш§БпжаЕФвЛЬѕБпЯрЧа?ШєДцдкЃЌЧыЧѓГі
Ш§БпжаЕФвЛЬѕБпЯрЧа?ШєДцдкЃЌЧыЧѓГі![]() ЕФжЕ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
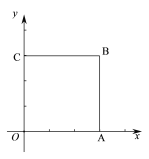
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌе§ЗНаЮOABCЕФЖЅЕуAЃЌCЗжБ№дкxжсЃЌyжсЩЯЃЌOA=3ЃЎ
ЃЈ1ЃЉЧѓжБЯпOBЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєжБЯпy=x+bгыИУе§ЗНаЮгаСНИіЙЋЙВЕуЃЌЧыжБНгаДГіbЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com