
分析 先求得其对称轴为x=-a,再分-a<-1、-1≤-a≤2和-a>2根据二次函数的单调性分别求得其最大值,由最大值为4,可求得a的值.
解答 解:
∵y=x2+2ax+1=(x+a)2+1-a2,
∴其对称为x=-a,开口向上,
当-a<-1,即a>1时,在-1≤x≤2上y随x的增大而增大,
∴当x=2时有最大值,最大值为4+4a+1,
∴5+4a=4,解得a=-$\frac{1}{4}$<1,不符合题意,舍去;
当-1≤-a≤2时,分两种情况,
①当-1≤-a≤$\frac{1}{2}$,即-$\frac{1}{2}$≤a≤1时,对称轴距离x=2远,
∴当x=2时函数有最大值,
∴4+4a+1=4,解得a=-$\frac{1}{4}$,
②当$\frac{1}{2}$≤-a≤2,即-2≤a≤-$\frac{1}{2}$时,对称轴距离x=-1远,
∴当x=-1时函数有最大值,最大值为2-2a,
∴2-2a=4,解得a=-1,
当-a>2,即a<-2时,在-1≤x≤2上,y随x的增大而减小,
∴当x=-1时,y有最大值,最大值为2-2a,
∴2-2a=4,解得a=-1>-2,不符合题意,舍去;
综上可知a的值为-$\frac{1}{4}$或-1.
点评 本题主要考查二次函数的单调性和最值,掌握二次函数的单调性是解题的关键,注意分类讨论思想的应用.


科目:初中数学 来源: 题型:解答题
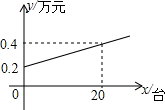 某商场负责空调销售的营销人员的工资结构是基本工资加销售提成,该商场5月份销售的甲、乙两种空调的进价和售价如表,而营销人员工资y与总销量x的函数图象如图所示:
某商场负责空调销售的营销人员的工资结构是基本工资加销售提成,该商场5月份销售的甲、乙两种空调的进价和售价如表,而营销人员工资y与总销量x的函数图象如图所示:| 甲 | 乙 | |
| 进价(万元/台) | 0.4 | 0.5 |
| 售价(万元/台) | 0.55 | 0.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com