Question

7．如图1，在正方形ABCD中，点P为AD延长线上一点，连接AC、CP，过点C作CF⊥CP交于C，交AB于点F，过点B作BM⊥CF于点N，交AC于点M．
（1）若AP=$\frac{7}{8}$AC，BC=4，求S_△ACP；
（2）若CP-BM=2FN，求证：BC=MC；
（3）如图2，在其他条件不变的情况下，将“正方形ABCD”改为“矩形ABCD”，且AB≠BC，AC=AP，取CP中点E，连接EB，交AC于点O，猜想：∠AOB与∠ABM之间有何数量关系？请说明理由．

Answer 1

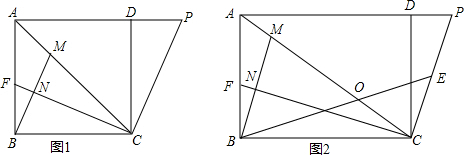
分析 （1）由正方形的性质得出AB=BC=CD=4，∠ADC=∠CDP=∠ABC=∠BCD=90°，由勾股定理求出AC，得出AP，即可求出S_△ACP；
（2）在CF上截取NG=FN，连接BG，则CF-CG=2FN，证出∠BCF=∠DCP，由ASA证明△BCF≌△DCP，得出CF=CP，证出CG=BM，由SAS证明△ABM≌△BCG，得出∠AMB=∠BGC，因此∠BMC=∠BGF，由线段垂直平分线的性质得出BF=BG，得出∠BFG=∠BGF，因此∠BMC=∠CBM，即可得出结论；
（3）连接AE，先证出∠BCA=2∠PAE，再证明∴A、D、E、C四点共圆，由圆周角定理得出∠DCP=∠PAE，得出∠BCF=∠PAE，证出∠BCA=2∠ABM，然后由三角形的外角性质即可得出结论．

解答 （1）解：∵四边形ABC是正方形，
∴AD∥BC，AB=BC=CD=4，∠ADC=∠CDP=∠ABC=∠BCD=90°，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=4$\sqrt{2}$，
∴AP=$\frac{7}{8}$AC=$\frac{7}{8}$×4$\sqrt{2}$=$\frac{7\sqrt{2}}{2}$，
∴S_△ACP=$\frac{1}{2}$AP×CD=$\frac{1}{2}$×$\frac{7\sqrt{2}}{2}$×4=7$\sqrt{2}$；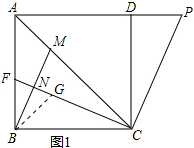
（2）证明：在CF上截取NG=FN，连接BG，如图1所示：
则CF-CG=2FN，
∵CF⊥CP，
∴∠PCF=90°，
∴∠BCF=∠DCP，
在△BCF和△DCP中，$\left\{\begin{array}{l}{∠ABC=∠CDP}&{\;}\\{BC=DC}&{\;}\\{∠BCF=∠DCP}&{\;}\end{array}\right.$，
∴△BCF≌△DCP（ASA），
∴CF=CP，
∵CP-BM=2FN，
∴CG=BM，
∵∠ABC=90°，BM⊥CF，
∴∠ABM=∠BCG，∠BFG=∠CBM，
在△ABM和△BCG中，$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠ABM=∠CBG}&{\;}\\{BM=CG}&{\;}\end{array}\right.$，
∴△ABM≌△BCG（SAS），
∴∠AMB=∠BGC，
∴∠BMC=∠BGF，
∵GN=FN，BM⊥CF，
∴BF=BG，
∴∠BFG=∠BGF，
∴∠BMC=∠CBM，
∴BC=MC；
（3）解：∠AOB=3∠ABM；理由如下：
连接AE并延长，交BC的延长线于点G，如图2所示：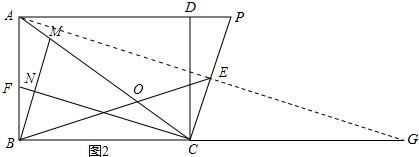

∵AC=AP，E是CP的中点，
∴AE⊥CP，PE=CE，∠PAE=∠CAE，
∵AD∥BC，
∴∠BCA=∠PAC=2∠PAE，∠PAE=∠G，
∴△APE≌△GCE，
∴AE=GE，
∵CP是AG的垂直平分线，
∴BE=GE，
∴∠G=∠CBE，
∵CF⊥CP，
∴AG∥FC，
∴∠G=∠BCF，
∵∠PCF=90°，∠BCD=90°，
∴∠BCF=∠DCP，
∴∠CBE=∠BCF，
∵∠ABM+∠BFC=90°，∠BCF+∠BFC=90°，
∴∠ABM=∠BCF，
∴∠CBE=∠ABM．
∵∠DCP+∠P=90°，∠PAE+∠P=90°，
∴∠DCP=∠PAE，
∴∠BCF=∠PAE，
∴∠ABM=∠BCF=∠PAE，
∴∠BCA=2∠ABM，
∵∠AOB=∠CBE+∠BCA，
∴∠AOB=3∠ABM．

点评 本题是四边形综合题目，考查了正方形的性质、勾股定理、全等三角形的判定与性质、线段垂直平分线的性质、等腰三角形的判定与性质、四点共圆、圆周角定理等知识；本题综合性强，有一定难度，特别是（2）中，需要通过作辅助线两次证明三角形全等才能得出结论．