
【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(![]() ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表8.
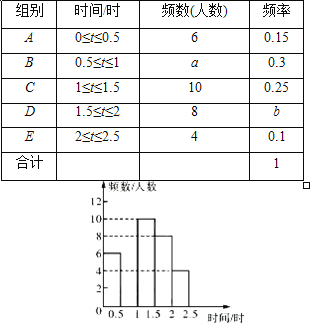
请根据图表中的信息,解答下列问题:
(1)表中的a=______,b=______,中位数落在________组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出2人向全校同学作读书心得报告,请用画树状图或列表法求抽取的2名学生刚好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,点
,点![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)写出点![]() 所在直线的函数解析式;
所在直线的函数解析式;
(2)连接![]() ,若线段
,若线段![]() 能构成三角形,求
能构成三角形,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 把四边形
把四边形![]() 的面积分成相等的两部分,试求
的面积分成相等的两部分,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级的三位老师带部分学生去红色旅游,联系了甲、乙两家旅行社,甲旅行社说:“带队老师免费,学生可以打8折.”乙旅行社说:“包括老师在内全部七折.”若全程费用每人200元.
(1)设有![]() 名学生参加活动,请分别写出参加两家旅行社的费用;
名学生参加活动,请分别写出参加两家旅行社的费用;
(2)若有25名学生参加活动,选择哪家旅行社更合算?
(3)计算21名和15名学生参加活动时,两家旅行社的费用分别是多少?根据上面的结果应如何选择哪家旅行社更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,….则顶点M2014的坐标为_______.
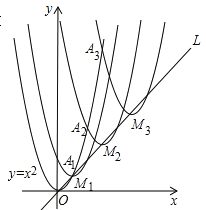
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2![]() ,∠DAO=30°,则FC的长度为( )
,∠DAO=30°,则FC的长度为( )
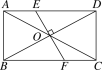
A. 1B. 2
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
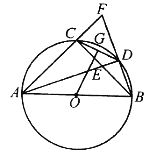
【题目】如图, ![]() 内接于⊙
内接于⊙![]() ,
, ![]() ,
, ![]() 的平分线
的平分线![]() 与⊙
与⊙![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,延长
,延长![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,
, ![]() 是
是![]() 的中点,连接
的中点,连接![]() .
.
(1)判断![]() 与
与![]() 的位置关系,写出你的结论并证明;
的位置关系,写出你的结论并证明;
(2)求证: ![]() ;
;
(3)若![]() ,求⊙
,求⊙![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com