
分析 根据分式的定义即可构造一个分式,然后取一个使得分式有意义的值代入即可.
解答 解:$\frac{{a}^{2}-1}{{a}^{2}-2a+1}$=$\frac{(a+1)(a-1)}{(a-1)^{2}}$=$\frac{a+1}{a-1}$,
当a=2时,原式=$\frac{2+1}{2-1}$=3.
或$\frac{{a}^{2}-2a+1}{{a}^{2}-1}$=$\frac{a-1}{a+1}$,
当a=2时,原式=$\frac{2-1}{2+1}$=$\frac{1}{3}$.
点评 本题考查分式的定义,分式的约分,理解题意是解题的关键,取值时注意使得分式有意义.


科目:初中数学 来源: 题型:选择题
| A. | 121(1+x)=100 | B. | 121(1-x)=100 | C. | 121(1-x)2=100 | D. | 100(1+x)2=121 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
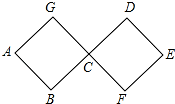 如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.
如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com