
【题目】在平面直角坐标系![]() 中,将-块含有
中,将-块含有![]() 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
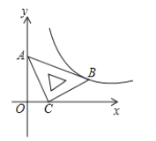
,顶点![]() 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿![]() 轴正方向平移,当顶点
轴正方向平移,当顶点![]() 恰好落在该双曲线上时停止运动,则此时点
恰好落在该双曲线上时停止运动,则此时点![]() 的对应点
的对应点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据三角形全等,可以求出点B的坐标,进而求出反比例函数的关系式,从而确定点A对应在双曲线上的点A′,从点A到点A′平移的距离就是点C到点C′的距离,最后确定点 C′的坐标.
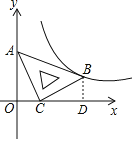
解:如图,过点B作BD⊥x轴,垂足为D,
∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∴∠OAC=∠BCD,
在△AOC和△CDB中,
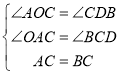 ,
,
∴△AOC≌△CDB (AAS)
∴OA=CD=4,OC=BD=2,
∴B(6,2)
点B在反比例函数![]() 的图象上,
的图象上,
∴k=12,
∴反比例函数的关系式为:![]() ,
,
当y=4时,即:4=![]() ,解得:x=3,
,解得:x=3,
因此点A向右平移3个单位,落在反比例函数的图象上,
故点C也相应向右平移3个单位,
∴点C′(5,0),
故选D.


科目:初中数学 来源: 题型:
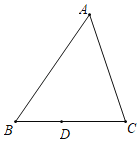
【题目】如图的![]() 中,
中,![]() ,且
,且![]() 为
为![]() 上一点.今打算在
上一点.今打算在![]() 上找一点
上找一点![]() ,在
,在![]() 上找一点
上找一点![]() ,使得
,使得![]() 与
与![]() 全等,以下是甲、乙两人的作法:
全等,以下是甲、乙两人的作法:
(甲)连接![]() ,作
,作![]() 的中垂线分别交
的中垂线分别交![]() 、
、![]() 于
于![]() 点、
点、![]() 点,则
点,则![]() 、
、![]() 两点即为所求
两点即为所求
(乙)过![]() 作与
作与![]() 平行的直线交
平行的直线交![]() 于
于![]() 点,过
点,过![]() 作与
作与![]() 平行的直线交
平行的直线交![]() 于
于![]() 点,则
点,则![]() 、
、![]() 两点即为所求
两点即为所求
对于甲、乙两人的作法,下列判断何者正确?( )
A. 两人皆正确B. 两人皆错误
C. 甲正确,乙错误D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明站在某广场一看台C处,从眼睛D处测得广场中心F的俯角为21°,若CD=1.6米,BC=1.5米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10米,则看台底端A点距离广场中心F点的距离约为(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)( )
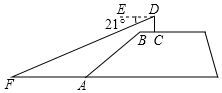
A.8.8米B.9.5米C.10.5米D.12米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有![]() 个分别标有数
个分别标有数![]() 的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为
的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为![]() ,小颖在剩下的
,小颖在剩下的![]() 个球中随机摸出一个小球记下数为
个球中随机摸出一个小球记下数为![]() ,这样确定了点
,这样确定了点![]() 的坐标.
的坐标.![]()
(1)请你利用列表法或画树状图法求点![]() 的横、纵坐标均能被
的横、纵坐标均能被![]() 整除的概率.
整除的概率.
(2)记点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求点
,求点![]() 位于反比例函数
位于反比例函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c的对称轴为直线x=1,且经过点(﹣1,0).若关于x的一元二次方程x2+bx+c﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,点A(0,3)与点B关于x轴对称,点C(n,0)为x轴的正半轴上一动点.以AC为边作等腰直角三角形ACD,∠ACD=90°,点D在第一象限内.连接BD,交x轴于点F.
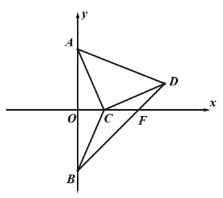
(1)如果∠OAC=38°,求∠DCF的度数;
(2)用含n的式子表示点D的坐标;
(3)在点C运动的过程中,判断OF的长是否发生变化?若不变求出其值,若变化请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com