
【题目】如图,![]() 为
为![]() 平分线,
平分线,![]() ,以
,以![]() 的长为直径作
的长为直径作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
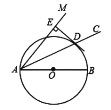
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)若![]() ,
,![]() 的长=_____.
的长=_____.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,根据AC为∠BAM的平分线以及OA=OD得到∠MAC=∠ADO,从而得出AE∥OD,结合DE⊥AM即可解答.
(2)过点D作DF⊥AB于点F,即可证得DE=DF=6,在Rt△ADF中利用射影定理求得AF,然后利用勾股定理求出AD.
(1)证明:连接OD,
∵AC为∠BAM的平分线,
∴∠BAC=∠MAC,
∵OA=OD,
∴∠BAC=∠ADO,
∴∠MAC=∠ADO
∴AE∥OD,
∵DE⊥AM,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:连接BD,过点D作DF⊥AB于点F,
∵AC为∠BAM平分线,DE⊥AM,
∴DF=DE=6,
∵AB是直径,![]() ,
,
∴∠ADB=90°,
∴DF2=AFBF,即62=AF(13AF),
∴AF=9或AF=4(舍去)
∴AD=![]() .
.
故答案为:![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的函数解析式为
的函数解析式为![]() ,点
,点![]() 是二次函数
是二次函数![]() 的图象上一点,过点
的图象上一点,过点![]() 作直线
作直线![]() 轴,且点
轴,且点![]() 的横坐标为
的横坐标为![]() ,二次函数
,二次函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象关于直线
的图象关于直线![]() 成轴对称.
成轴对称.

(1)直接写出二次函数![]() 图象的对称轴(用含
图象的对称轴(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落在
落在![]() 轴上时,求二次函数
轴上时,求二次函数![]() 的解析式.
的解析式.
(3)当点![]() 在
在![]() 轴的右侧时,过点
轴的右侧时,过点![]() 作射线
作射线![]() 轴,设射线
轴,设射线![]() 与
与![]() 的图象交于点
的图象交于点![]() ,
,![]() 的图象在
的图象在![]() 上方的部分记为
上方的部分记为![]() ,
,![]() 的图象的剩余部分沿
的图象的剩余部分沿![]() 翻折得到
翻折得到![]() ,由
,由![]() 和
和![]() 所组成的图象记为
所组成的图象记为![]() .
.
①当点![]() 的纵坐标与横坐标之和为6时,求
的纵坐标与横坐标之和为6时,求![]() 的值
的值
②当![]() 时,随着
时,随着![]() 的增大,图象
的增大,图象![]() 所对应函数的函数值
所对应函数的函数值![]() 先减小后增大时,直接写出
先减小后增大时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
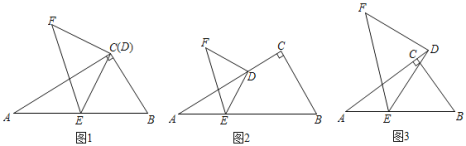
【题目】观察猜想:
(1)如图1,在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D与点C重合,点E在斜边AB上,连接DE,且DE=AE,将线段DE绕点D顺时针旋转90°得到线段DF,连接EF,则![]() =______,sin∠ADE=________,
=______,sin∠ADE=________,
探究证明:
(2)在(1)中,如果将点D沿CA方向移动,使CD=![]() AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由.
AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由.
拓展延伸
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=a,点D在边AC的延长线上,E是AB上任意一点,连接DE.ED=nAE,将线段DE绕着点D顺时针旋转90°至点F,连接EF.求![]() 和sin∠ADE的值分别是多少?(请用含有n,a的式子表示)
和sin∠ADE的值分别是多少?(请用含有n,a的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位正整数数m,若其千位与百位上的数字之和为9,十位与个位上的数字之和也为9,那么称m为“重九数”,如:1827、3663.将“重九数”m的千位数字与十位数字对调,百位数字与个位数字对调,得到一个新的四位正整数数n,如:m=2718,则n=1827,记D(m,n)=m+n.
(1)请写出两个四位“重九数”: , .
(2)求证:对于任意一个四位“重九数”m,其D(m,n)可被101整除.
(3)对于任意一个四位“重九数”m,记f(m,n)=![]() ,当f(m,n)是一个完全平方数时,且满足m>n,求满足条件的m的值.
,当f(m,n)是一个完全平方数时,且满足m>n,求满足条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.事件“在一张纸上随意画两个直角三角形,这两个直角三角形相似”是确定事件
B.如果一组数据为![]() ,其平均数为
,其平均数为![]() 那么这组数据的方差为
那么这组数据的方差为![]()
C.事件“若![]() 的面积是
的面积是![]() ,则它的一边长
,则它的一边长![]() 与这边上的高h的函数关系式为
与这边上的高h的函数关系式为![]() ”是随机事件
”是随机事件
D.从一个装有![]() 个红球和
个红球和![]() 个黑球的袋子中任取一球,取到的是黑球符合如右图所示的“用频率估计概率”的实验得出的频率折线图(如图)
个黑球的袋子中任取一球,取到的是黑球符合如右图所示的“用频率估计概率”的实验得出的频率折线图(如图)

查看答案和解析>>
科目:初中数学 来源: 题型:
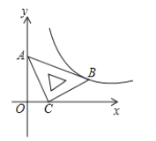
【题目】在平面直角坐标系![]() 中,将-块含有
中,将-块含有![]() 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿![]() 轴正方向平移,当顶点
轴正方向平移,当顶点![]() 恰好落在该双曲线上时停止运动,则此时点
恰好落在该双曲线上时停止运动,则此时点![]() 的对应点
的对应点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
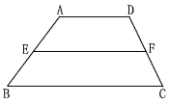
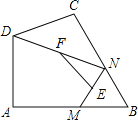
【题目】(1)如图,已知△ABC中,D、E分别是AB、AC的中点,求证:DE∥BC,DE=![]() BC.
BC.
(2)利用第(1)题的结论,解决下列问题:
①如图,在四边形ABCD中,AD∥BC,E、F分别是AB、CD的中点,求证:EF∥BC,FE=![]() (AD+BC)
(AD+BC)
②如图,在四边形ABCD中,∠A=90°,AB=3![]() ,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,求EF长度的最大值.
,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,求EF长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com