
【题目】对任意一个四位正整数数m,若其千位与百位上的数字之和为9,十位与个位上的数字之和也为9,那么称m为“重九数”,如:1827、3663.将“重九数”m的千位数字与十位数字对调,百位数字与个位数字对调,得到一个新的四位正整数数n,如:m=2718,则n=1827,记D(m,n)=m+n.
(1)请写出两个四位“重九数”: , .
(2)求证:对于任意一个四位“重九数”m,其D(m,n)可被101整除.
(3)对于任意一个四位“重九数”m,记f(m,n)=![]() ,当f(m,n)是一个完全平方数时,且满足m>n,求满足条件的m的值.
,当f(m,n)是一个完全平方数时,且满足m>n,求满足条件的m的值.
【答案】(1)3645,7263;(2)见解析;(3)9054、8163、6318、5427、4536
【解析】
(1)根据“重九数“定义写出两个符合要求的数即可;
(2)将m的各个数位上的数字用字母表示,得出D(m,n)的表达式,一定有因数101;
(3)先得出f(m,n)的表达式,再根据完全平方数的特征得出不定方程,解不定方程即可求出m的值.
解:(1)根据“重九数“定义写出两个符合要求的数即可,3645,7263,(答案不唯一,符合题意即可),
故答案为:3645,7263;
(2)证明:设任意一个“重九数“m为![]() ,(a,b,c,d均为1~9的自然数),则n为
,(a,b,c,d均为1~9的自然数),则n为![]() ,
,
∴D(m,n)=m+n=1000a+100b+10c+d+1000c+100d+10a+b=101(10a+10c+b+d),
∴D(m,n)可被101整除;
(3)由(2)可知,对于任意的“重九数“m=![]() ,有D(m,n)=101(10a+10c+b+d),
,有D(m,n)=101(10a+10c+b+d),
∴f(m,n)=10a+10c+b+d,
∵a+b=9,c+d=9,
∴b=9﹣a,d=9﹣c,
∴f(m,n)=10a+10c+b+d=10a+10c+9﹣a+9﹣c=9a+9c+18=9(a+c+2),
∵f(m,n)是完全平方数,9是完全平方数,
∴a+c+2是完全平方数,
∵1≤a≤9,1≤c≤9,且m>n,
∴a>c,5≤a+c+2≤19,
∴a+c+2=9或16,
当a+c+2=9时,解得![]() 或
或![]() 或
或![]() .
.
当a+c+2=16时,解得![]() 或
或![]() .
.
综上所述,满足要求的m的值有:9054、8163、6318、5427、4536.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】为了让学生掌握知识更加牢固,某校九年级物理组老师们将物理实验的教学方式由之前的理论教学改进为理论+实践,一段时间后,从九年级随机抽取15名学生,对他们在教学方式改进前后的物理实验成绩(百分制)进行整理、描述和分析(成绩用![]() 表示,共分成4组:A.
表示,共分成4组:A.![]() ,B.
,B.![]() ,C.
,C.![]() ,D.
,D.![]() ),下面给出部分信息:
),下面给出部分信息:
教学方式改进前抽取的学生的成绩在![]() 组中的数据为:80,83,85,87,89.
组中的数据为:80,83,85,87,89.
教学方式改进后抽取的学生成绩为:72,70,76,100,98,100,82,86,95,90,100,86,84,93,88.
教学方式改进前抽取的学生成绩频数分布直方图
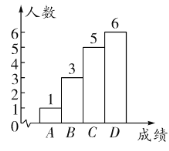
教学方式改进前后抽取的学生成绩对比统计表
统计量 | 改进前 | 改进后 |
平均数 | 88 | 88 |
中位数 |
|
|
众数 | 98 |
|
根据以上信息,解答下列问题:
(1)直接写出上述图表中![]() 的值;
的值;
(2)根据以上数据,你认为该校九年级学生的物理实验成绩在教学方式改进前好,还是改进后好?请说明理由(一条理由即可);
(3)若该校九年级有300名学生,规定物理实验成绩在90分及以上为优秀,估计教学方式改进后成绩为优秀的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
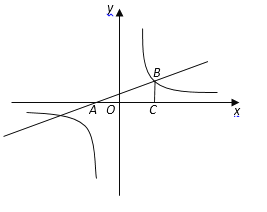
【题目】如图,平面直角坐标系中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 在第一象限内交于点B,BC丄x轴于点C,OC=2AO.
在第一象限内交于点B,BC丄x轴于点C,OC=2AO.
(1)求双曲线的解析式.
(2)点D为y轴上一个动点,若S△ADB=3,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明站在某广场一看台C处,从眼睛D处测得广场中心F的俯角为21°,若CD=1.6米,BC=1.5米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10米,则看台底端A点距离广场中心F点的距离约为(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)( )
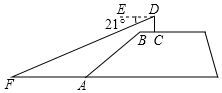
A.8.8米B.9.5米C.10.5米D.12米
查看答案和解析>>
科目:初中数学 来源: 题型:
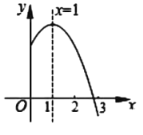
【题目】已知二次函数![]() (
(![]() 是常数,
是常数,![]() )图象的对称轴是直线
)图象的对称轴是直线![]() ,其图象的一部分如图所示,下列说法中①
,其图象的一部分如图所示,下列说法中①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④
;④![]() ;⑤
;⑤![]() .正确的结论有( )
.正确的结论有( )
A.①②④B.②③④C.①③⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
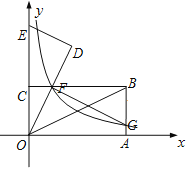
【题目】在如图平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),OA、OC分别落在x轴和y轴上,OB是矩形的对角线.将△OAB绕点O逆时针旋转,使点B落在y轴上,得到△ODE,OD与CB相交于点F,反比例函数y=![]() (x>0)的图象经过点F,交AB于点G.
(x>0)的图象经过点F,交AB于点G.
(1)求k的值和点G的坐标;
(2)连接FG,则图中是否存在与△BFG相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由;
(3)在线段OA上存在这样的点P,使得△PFG是等腰三角形.请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com