
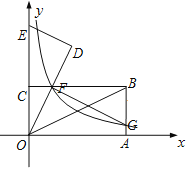
【题目】在如图平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),OA、OC分别落在x轴和y轴上,OB是矩形的对角线.将△OAB绕点O逆时针旋转,使点B落在y轴上,得到△ODE,OD与CB相交于点F,反比例函数y=![]() (x>0)的图象经过点F,交AB于点G.
(x>0)的图象经过点F,交AB于点G.
(1)求k的值和点G的坐标;
(2)连接FG,则图中是否存在与△BFG相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由;
(3)在线段OA上存在这样的点P,使得△PFG是等腰三角形.请直接写出点P的坐标.
【答案】(1)k=2,点G的坐标为(4,![]() );(2)△COF∽△BFG;△AOB∽△BFG;△ODE∽△BFG;△CBO∽△BFG,证明详见解析;(3)点P的坐标为(4﹣
);(2)△COF∽△BFG;△AOB∽△BFG;△ODE∽△BFG;△CBO∽△BFG,证明详见解析;(3)点P的坐标为(4﹣![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)证明△COF∽△AOB,则![]() ,求得:点F的坐标为(1,2),即可求解;
,求得:点F的坐标为(1,2),即可求解;
(2)△COF∽△BFG;△AOB∽△BFG;△ODE∽△BFG;△CBO∽△BFG.证△OAB∽△BFG:![]() ,
,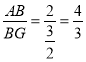 ,即可求解.
,即可求解.
(3)分GF=PF、PF=PG、GF=PG三种情况,分别求解即可.
解:(1)∵四边形OABC为矩形,点B的坐标为(4,2),
∴∠OCB=∠OAB=∠ABC=90°,OC=AB=2,OA=BC=4,
∵△ODE是△OAB旋转得到的,即:△ODE≌△OAB,
∴∠COF=∠AOB,∴△COF∽△AOB,
∴![]() ,∴
,∴![]() =
=![]() ,∴CF=1,
,∴CF=1,
∴点F的坐标为(1,2),
∵y=![]() (x>0)的图象经过点F,
(x>0)的图象经过点F,
∴2=![]() ,得k=2,
,得k=2,
∵点G在AB上,
∴点G的横坐标为4,
对于y=![]() ,当x=4,得y=
,当x=4,得y=![]() ,
,
∴点G的坐标为(4,![]() );
);
(2)△COF∽△BFG;△AOB∽△BFG;△ODE∽△BFG;△CBO∽△BFG.
下面对△OAB∽△BFG进行证明:
∵点G的坐标为(4,![]() ),∴AG=
),∴AG=![]() ,
,
∵BC=OA=4,CF=1,AB=2,
∴BF=BC﹣CF=3,
BG=AB﹣AG=![]() .
.
∴![]() ,
,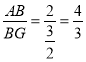 .
.
∴![]() ,
,
∵∠OAB=∠FBG=90°,
∴△OAB∽△FBG.
(3)设点P(m,0),而点F(1,2)、点G(4,![]() ),
),
则FG2=9+![]() =
=![]() ,PF2=(m﹣1)2+4,PG2=(m﹣4)2+
,PF2=(m﹣1)2+4,PG2=(m﹣4)2+![]() ,
,
当GF=PF时,即![]() =(m﹣1)2+4,解得:m=
=(m﹣1)2+4,解得:m=![]() (舍去负值);
(舍去负值);
当PF=PG时,同理可得:m=![]() ;
;
当GF=PG时,同理可得:m=4﹣![]() ;
;
综上,点P的坐标为(4﹣![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】对任意一个四位正整数数m,若其千位与百位上的数字之和为9,十位与个位上的数字之和也为9,那么称m为“重九数”,如:1827、3663.将“重九数”m的千位数字与十位数字对调,百位数字与个位数字对调,得到一个新的四位正整数数n,如:m=2718,则n=1827,记D(m,n)=m+n.
(1)请写出两个四位“重九数”: , .
(2)求证:对于任意一个四位“重九数”m,其D(m,n)可被101整除.
(3)对于任意一个四位“重九数”m,记f(m,n)=![]() ,当f(m,n)是一个完全平方数时,且满足m>n,求满足条件的m的值.
,当f(m,n)是一个完全平方数时,且满足m>n,求满足条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知△ABC中,D、E分别是AB、AC的中点,求证:DE∥BC,DE=![]() BC.
BC.
(2)利用第(1)题的结论,解决下列问题:
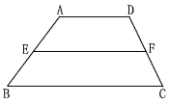
①如图,在四边形ABCD中,AD∥BC,E、F分别是AB、CD的中点,求证:EF∥BC,FE=![]() (AD+BC)
(AD+BC)
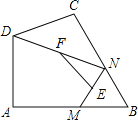
②如图,在四边形ABCD中,∠A=90°,AB=3![]() ,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,求EF长度的最大值.
,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,求EF长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
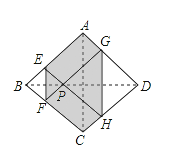
【题目】如图,正方形纸片![]() 的边长为
的边长为![]() ,翻折
,翻折![]() ,使两个直角顶点重合于对角线
,使两个直角顶点重合于对角线![]() 上一点
上一点![]() 分别是折痕,设
分别是折痕,设![]() ,给出下列判断:
,给出下列判断:
①当![]() 时,点
时,点![]() 是正方形
是正方形![]() 的中心;
的中心;
②当![]() 时,
时,![]() ;
;
③当![]() 时,六边形
时,六边形![]() 面积的最大值是
面积的最大值是![]()
④当![]() 时,六边形
时,六边形![]() 周长的值不变.
周长的值不变.
其中错误的是( )
A.②③B.③④C.①④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
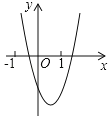
【题目】抛物线y=ax2+bx+c的图象如图所示,那么一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致是( )
在同一坐标系内的图象大致是( )
A.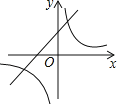 B.
B.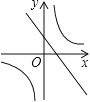
C.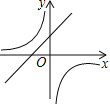 D.
D.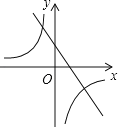
查看答案和解析>>
科目:初中数学 来源: 题型:
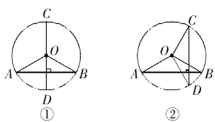
【题目】在⊙O中,AB是非直径弦,弦CD⊥AB,
(1)当CD经过圆心时(如图①),∠AOC+∠DOB=__________;
(2)当CD不经过圆心时(如图②),∠AOC+∠DOB的度数与(1)的情况相同吗?试说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
已知:直线![]() 及直线
及直线![]() 外一点P.
外一点P.

求作:直线![]() ,使
,使![]() .
.
作法:如图,
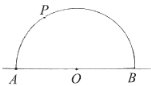
①在直线![]() 上取一点O,以点O为圆心,
上取一点O,以点O为圆心,![]() 长为半径画半圆,交直线
长为半径画半圆,交直线![]() 于
于![]() 两点;
两点;
②连接![]() ,以B为圆心,
,以B为圆心,![]() 长为半径画弧,交半圆于点Q;
长为半径画弧,交半圆于点Q;
③作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小明设计的尺规作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明
证明:连接![]() ,
,
∵![]() ,
,
∴![]() __________.
__________.
∴![]() (______________)(填推理的依据).
(______________)(填推理的依据).
∴![]() (_____________)(填推理的依据).
(_____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
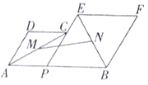
【题目】如图,AB=4,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE的中点.当点P在线段AB上移动时,点M,N之间的距离最短为( ).
A.![]() B.
B.![]() C.2D.3
C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com